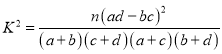题目内容
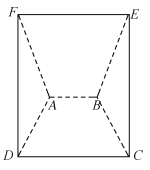
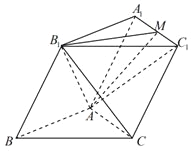
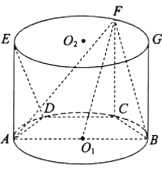
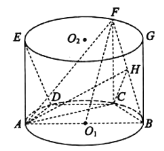
【题目】在如图所示的圆柱![]() 中,AB为圆
中,AB为圆![]() 的直径,
的直径,![]() 是
是![]() 的两个三等分点,EA,FC,GB都是圆柱
的两个三等分点,EA,FC,GB都是圆柱![]() 的母线.
的母线.
(1)求证:![]() 平面ADE;
平面ADE;
(2)设BC=1,已知直线AF与平面ACB所成的角为30°,求二面角A—FB—C的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)由![]() ,另易证得
,另易证得![]() ,即可证得面
,即可证得面![]() 面
面![]() ,由面面平行,从而证得线面平行,即
,由面面平行,从而证得线面平行,即![]() 面
面![]() .
.
(2)连接![]() ,易证
,易证![]() 面
面![]() ,可过
,可过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 即为二面角A—FB—C的平面角,求出其余弦值即得.
即为二面角A—FB—C的平面角,求出其余弦值即得.
解:(1)连接![]() ,因为C,D是半圆
,因为C,D是半圆![]() 的两个三等分点,
的两个三等分点,
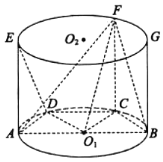
所以![]() ,
,
又![]() ,
,
所以![]() 均为等边三角形.
均为等边三角形.
所以![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又因为![]() 平面ADE,
平面ADE,![]() 平面ADE,所以
平面ADE,所以![]() 平面ADE.
平面ADE.
因为EA,FC都是圆柱![]() 的母线,所以EA//FC.
的母线,所以EA//FC.
又因为![]() 平面ADE,
平面ADE,![]() 平面ADE,
平面ADE,
所以![]() 平面ADE. 又
平面ADE. 又![]() 平面
平面![]() ,
,
所以平面![]() 平面ADE,又
平面ADE,又![]() 平面
平面![]() ,所以
,所以![]() 平面ADE.
平面ADE.
(2)连接AC,因为FC是圆柱![]() 的母线,所以
的母线,所以![]() 圆柱
圆柱![]() 的底面,
的底面,
所以![]() 即为直线AF与平面ACB所成的角,即
即为直线AF与平面ACB所成的角,即![]()
因为AB为圆![]() 的直径,所以
的直径,所以![]() ,
,
在![]() ,
,
所以![]() ,所以在
,所以在![]()
因为![]() ,又因为
,又因为![]() ,所以
,所以![]() 平面FBC,
平面FBC,
又![]() 平面FBC,所以
平面FBC,所以![]() .
.
在![]() 内,作
内,作![]() 于点H,连接AH.
于点H,连接AH.
因为![]() 平面ACH,所以
平面ACH,所以![]() 平面ACH,
平面ACH,
又![]() 平面ACH,所以
平面ACH,所以![]() ,
,
所以![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
在![]() ,在
,在![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

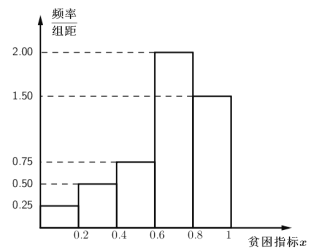
【题目】携号转网,也称作号码携带、移机不改号,即无需改变自己的手机号码,就能转换运营商,并享受其提供的各种服务.2019年11月27日,工信部宣布携号转网在全国范围正式启动.某运营商为提质量保客户,从运营系统中选出300名客户,对业务水平和服务水平的评价进行统计,其中业务水平的满意率为![]() ,服务水平的满意率为
,服务水平的满意率为![]() ,对业务水平和服务水平都满意的客户有180人.
,对业务水平和服务水平都满意的客户有180人.
(Ⅰ)完成下面![]() 列联表,并分析是否有
列联表,并分析是否有![]() 的把握认为业务水平与服务水平有关;
的把握认为业务水平与服务水平有关;
对服务水平满意人数 | 对服务水平不满意人数 | 合计 | |
对业务水平满意人数 | |||
对业务水平不满意人数 | |||
合计 |
(Ⅱ)为进一步提高服务质量,在选出的对服务水平不满意的客户中,抽取2名征求改进意见,用![]() 表示对业务水平不满意的人数,求
表示对业务水平不满意的人数,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)若用频率代替概率,假定在业务服务协议终止时,对业务水平和服务水平两项都满意的客户流失率为![]() ,只对其中一项不满意的客户流失率为
,只对其中一项不满意的客户流失率为![]() ,对两项都不满意的客户流失率为
,对两项都不满意的客户流失率为![]() ,从该运营系统中任选4名客户,则在业务服务协议终止时至少有2名客户流失的概率为多少?
,从该运营系统中任选4名客户,则在业务服务协议终止时至少有2名客户流失的概率为多少?
附: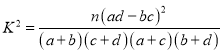 ,
,![]() .
.
0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |