题目内容
【题目】已知![]() 元集合
元集合![]() 的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为
的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为![]() .问:是否存在不小于3的正整数
.问:是否存在不小于3的正整数![]() ,使
,使![]() 的最大值等于2009的方幂?说明你的理由.
的最大值等于2009的方幂?说明你的理由.
【答案】见解析
【解析】
设![]() 取最大值时,对应有
取最大值时,对应有![]() 个子集
个子集![]() .则
.则![]() .
.
若存在某个![]() ,使
,使![]() ,不妨设为
,不妨设为![]() ,将
,将![]() 的所有三元子集记为
的所有三元子集记为![]() ,则
,则![]() .
.
对任意的![]() ,有
,有![]() .
.
对任意的![]() ,有
,有![]() .
.
由已知,对任意的![]() ,
,![]() ,有
,有
![]() .
.
故可用![]() 替换原先的
替换原先的![]() ,形成新的子集族.
,形成新的子集族.
因![]()
![]() ,
,
所以,替换后所有集合元素个数的立方和增加,这与![]() 的最大性矛盾.
的最大性矛盾.
于是,当![]() 取最大值时,每个子集元素的个数都不大于3.
取最大值时,每个子集元素的个数都不大于3.
又取一切![]() 的二元子集和三元子集形成的子集族满足题意,于是,它们的元素个数的立方和为
的二元子集和三元子集形成的子集族满足题意,于是,它们的元素个数的立方和为![]()
![]()
![]() .
.
假设![]() .则
.则
![]() . ①
. ①
若![]() 是偶数,则
是偶数,则![]() 是偶数.从而,式①左边是4的倍数,矛盾.
是偶数.从而,式①左边是4的倍数,矛盾.
所以,![]() 是奇数.
是奇数.
记![]() ,则
,则
![]() 是10的约数.
是10的约数.
结合式①知![]() .
.
又因![]() ,
,![]() ,所以,当
,所以,当![]() 时,式①左边的三个因数的质因子互不相同,故只可能
时,式①左边的三个因数的质因子互不相同,故只可能![]() .此时,
.此时,![]() ,而式①右边不含质因子3,矛盾.
,而式①右边不含质因子3,矛盾.
综上,不存在不小于3的正整数![]() ,使
,使![]() 的最大值等于2009的方幂.
的最大值等于2009的方幂.

 阅读快车系列答案
阅读快车系列答案【题目】十九大指出,必须树立“绿水青山就是金山银山”的生态文明发展理念,这一理念将进一步推动新能源汽车产业的迅速发展![]() 以下是近几年我国新能源汽车的年销量数据及其散点图
以下是近几年我国新能源汽车的年销量数据及其散点图![]() 如图所示
如图所示![]() :
:
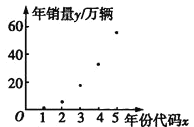
年份 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
新能源汽车的年销量 |
|
|
|
|
|
(1)请根据散点图判断![]() 与
与![]() 中哪个更适宜作为新能源汽车年销量
中哪个更适宜作为新能源汽车年销量![]() 关于年份代码
关于年份代码![]() 的回归方程模型?
的回归方程模型?![]() 给出判断即可,不必说明理由)
给出判断即可,不必说明理由)
(2)根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程,并预测2019年我国新能源汽车的年销量
的回归方程,并预测2019年我国新能源汽车的年销量![]() 精确到
精确到![]()
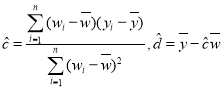
附令![]() ,
,
|
|
|
|
|
| 10 | 374 |
| 851.2 |
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如图,把该直方图所得频率估计为概率.

(1)请估算2019年(以365天计算)全年该区域空气质量优良的天数(未满一天按一天计算);
(2)该校2019年6月7、8日将作为高考考场,若这两天中某天出现5级重度污染,需要净化空气费用8000元,出现6级严重污染,需要净化空气费用12000元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
