题目内容
【题目】在箱子中有10个小球,其中有3个红球,3个白球,4个黑球.从这10个球中任取3个.求:
(1)取出的3个球中红球的个数![]() 的分布列;
的分布列;
(2)取出的3个球中红球个数多于白球个数的概率.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)优先表示随机变量可能的取值,显然该事件服从超几何分布,由其概率计算公式分别求得对应概率即可列出分布列;
(2)事件“红球个数多于白球个数” 可以分解为,“恰好取出![]() 个红球和
个红球和![]() 个黑球”为事件
个黑球”为事件![]() ,“恰好取出
,“恰好取出![]() 个红球”为事件
个红球”为事件![]() ,“恰好取出
,“恰好取出![]() 个红球”为事件
个红球”为事件![]() ,再由计数原理和古典概型概率公式分别计算概率,最后由相互独立事件的概率计算方式求得答案.
,再由计数原理和古典概型概率公式分别计算概率,最后由相互独立事件的概率计算方式求得答案.
(1)题意知![]() 的所有可能取值为
的所有可能取值为![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 服从参数为
服从参数为![]() ,
,![]() ,
,![]() 的超几何分布,
的超几何分布,
因此 ![]() .
.
所以 ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故 ![]() 的分布列为 :
的分布列为 :
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(2)设“取出的3个球中红球个数多于白球个数”为事件![]() ,“恰好取出
,“恰好取出![]() 个红球和
个红球和![]() 个黑球”为事件
个黑球”为事件![]() ,“恰好取出
,“恰好取出![]() 个红球”为事件
个红球”为事件![]() ,“恰好取出
,“恰好取出![]() 个红球”为事件
个红球”为事件![]() ,
,
由于事件![]() ,
,![]() ,
,![]() 彼此互斥,且
彼此互斥,且![]() ,
,
而![]() ,
,![]() ,
,![]() ,
,
所以取出的3个球中红球个数多于白球个数的概率为:
![]() .
.
答:取出的3个球中红球个数多于白球个数的概率为![]() .
.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱。现统计了连续5天的售出和收益情况,如下表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x与y成线性相关,则某天售出8箱水时,预计收益为多少元?
(Ⅱ) 期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前200名,获一等奖学金500元;考入年级201—500 名,获二等奖学金300元;考入年级501名以后的特困生将不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
⑴在学生甲获得奖学金条件下,求他获得一等奖学金的概率;
⑵已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额X 的分布列及数学期望。
附: 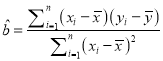 ,
, ![]() 。
。