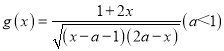题目内容
【题目】已知抛物线y2=2px的焦点为F,准线方程是x=﹣1.
(I)求此抛物线的方程;
(Ⅱ)设点M在此抛物线上,且|MF|=3,若O为坐标原点,求△OFM的面积.
【答案】(Ⅰ)y2=4x;(Ⅱ)![]()
【解析】
试题(I)利用准线方程是x=﹣1,求此抛物线的方程;
(Ⅱ)设点M在此抛物线上,且|MF|=3,利用抛物线的定义求出M的坐标,即可求△OFM的面积.
解:(Ⅰ)因为抛物线的准线方程为x=﹣1,
所以![]()
得p=2
所以,抛物线的方程为 y2=4x
(Ⅱ)设M(x0,y0),因为点M(x0,y0)在抛物线上,且|MF|=3,
由抛物线定义知|MF|=x0+![]() =3
=3
得x0=2
由M(2,y0)在抛物线上,满足抛物线的方程为y2=4x知y0=±2![]()
所以△OMP的面积为![]() |y0|=
|y0|=![]() =
=![]() .
.

练习册系列答案
相关题目