题目内容
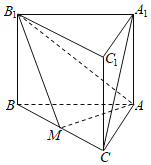
【题目】如图，直三棱柱ABC﹣A1B1C1，中，点M是棱BC的中点.
（2）求证：A1C∥平面AB1M；
（2）如果AB＝AC，求证AM⊥平面BCC1B1.
【答案】（1）见解析；（2）见解析
【解析】
（1）连结A1B，交AB1于M，连结MN，在三角形
中由中位线定理证得，线线平行，由线面平行的判定定理得证；
（2）由等腰三角形三线合一证得AM⊥BC，由直三棱柱证得BB1⊥底面ABC，进而证得AM⊥BB1，由线面垂直的判定定理得证.
（1）连结A1B，交AB1于M，连结MN，
∵直三棱柱ABC﹣A1B1C1中，点M是棱BC的中点.
∴N是A1B的中点，∴MN∥A1C，
∵MN平面AB1M，A1C平面AB1M，
∴A1C∥平面AB1M.
（2）∵AB＝AC，M是BC中点，
∴AM⊥BC，
∵直三棱柱ABC﹣A1B1C1中，BB1⊥底面ABC，AM平面ABC，
∴AM⊥BB1，
∵BC∩BB1＝B，∴AM⊥平面BCC1B1.
练习册系列答案
相关题目
