��Ŀ����
����Ŀ��ijѧУΪ����ȫ��ѧ��Ϊ����ѧ����������һԪǮ��һƬ�ģ�������ˮ�����ѧ���ڹ�ˮ��ÿ��ȡһƿ��Ȫˮ�����Ծ�������������Ͷ��һԪǮ����ͳ��������5����۳���������������±���
�۳�ˮ��x����λ���䣩 | 7 | 6 | 6 | 5 | 6 |
����y����λ��Ԫ�� | 165 | 142 | 148 | 125 | 150 |
(��) ��x��y��������أ���ij���۳�8��ˮʱ��Ԥ������Ϊ����Ԫ��
(��) ���п����Ժ�ѧУ������������ˮ�����棬�Խ�ѧ�����ʽ������Ʒѧ���ŵ����������涨�������������꼶ǰ200������һ�Ƚ�ѧ��500Ԫ�������꼶201��500 ��������Ƚ�ѧ��300Ԫ�������꼶501���Ժ��������������ý�ѧ�𡣼ס�������ѧ����һ�Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������Ƚ�ѧ��ĸ��ʾ�Ϊ
������Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������ý�ѧ��ĸ��ʾ�Ϊ
������ý�ѧ��ĸ��ʾ�Ϊ![]() .
.
����ѧ����ý�ѧ�������£��������һ�Ƚ�ѧ��ĸ��ʣ�
����֪�ס�������ѧ������ĸ��ȵڵĽ�ѧ����������ģ���ס�������ѧ������ý�ѧ���ܽ��X �ķֲ��м���ѧ������
���� 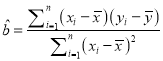 ��
�� ![]() ��
��
���𰸡�����186Ԫ������1��![]() ����2���ֲ��м�����������Ϊ600.
����2���ֲ��м�����������Ϊ600.
�����������������
(��)���������ûع鷽��Ϊ![]() ���ݴ�Ԥ���۳�8��ˮʱ��Ԥ������Ϊ186Ԫ��
���ݴ�Ԥ���۳�8��ˮʱ��Ԥ������Ϊ186Ԫ��
(��) (1)���������ʹ�ʽ�ɵ������һ�Ƚ�ѧ��ĸ�����![]() ��
��
(2) ������ɵ�X��ȡֵ����Ϊ0��300��500��600��800��1000���ݴ���÷ֲ��У�Ȼ�����ɵ���ѧ����Ϊ600.
���������
![]() ��
�� ![]()
 ��
�� ![]()
![]() ��
��
��![]() ʱ��
ʱ�� ![]()
��ij���۳�8��ˮ��Ԥ��������186Ԫ��
(��) �����¼�AΪ��ѧ����ý�ѧ�������¼�BΪ��ѧ�����һ�Ƚ�ѧ������

��ѧ����ý�ѧ��������£����һ�Ƚ�ѧ��ĸ���Ϊ![]()
��X��ȡֵ����Ϊ0��300��500��600��800��1000
![]() ��
��![]() ��
��![]()
![]() ��
��![]() ��
��![]()
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��

![]() ��Ԫ��
��Ԫ��