题目内容
6.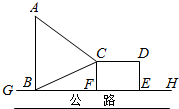 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm(1)求y关于x的函数解析式
(2)如果中转站四周围墙(即矩形周长)造价为2万元/km,两条道路造价为6万元/km,问:x取何值时,该公司建中转围墙和两条道路总造价M最低?
分析 (1)根据题意得AB=y且AC=y-1,在Rt△BCF中,BC=2CF=2x.然后在△ABC中利用余弦定理AC2=AB2+BC2-2•AB•BC•cosB的式子建立关于x、y的等式,解出用x表示y的式子,即可得到y关于x的函数解析式;
(2)由(1)求出的函数关系式,结合题意得出总造价M=12x2−3x−1-3+4x.然后换元:令x-1=t,化简得到M=16t+9t+25,利用基本不等式算出当t=34时,M的最小值为49.由此即可得出当总造价M最低时,相应的x值.
解答 解:(1)∵AB=y,AB=AC+1,∴AC=y-1.
∵在Rt△BCF中,CF=x,∠ABC=60°,
∴∠CBF=30°,可得BC=2x.
由于2x+y-1>y,得x>12.
在△ABC中,根据余弦定理AC2=AB2+BC2-2•AB•BC•cosB,
可得(y-1)2=y2+(2x)2-2(y-1)•2x•cos60°,
即(y-1)2=y2+4x2-2x(y-1),解得y=4x2−12(x−1).
∵y>0且x>12,
∴x>1.
可得y关于x的函数解析式为y=4x2−12(x−1)(x>1).
(2)由题意,可得总造价M=6[y+(y-1)]+8x-4=212x2−3x−1-10+8x.
令x-1=t,则M=2•12(t+1)2−3t-10+8(t+1)=32t+18t+46≥2√32t•18t+46=94,
当且仅当32t=18t,即t=34时,M的最小值为94.
此时x=t+1=74,y=4x2−12(x−1)=152.
答:当x的值为74时,该公司建中转站围墙和道路总造价M最低.
点评 本题给出实际应用问题,求能够使公司建中转站围墙和两条道路总造价最低的方案.着重考查了函数解析式的求法、运用基本不等式求最值和余弦定理及其应用等知识,属于中档题.

 天天向上口算本系列答案
天天向上口算本系列答案