题目内容
5.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象上相邻的两个最低点和最高点坐标分别为(-$\frac{π}{6}$,-2),($\frac{5π}{6}$,4).(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递减区间.
分析 (1)根据条件分别求出A,ω和φ的值,即可求函数f(x)的解析式;
(2)根据三角函数的单调性即可求函数f(x)的单调递减区间.
解答 解:(1)设f(x)的最小正周期为T,得T=2($\frac{5π}{6}$+$\frac{π}{6}$)=2π,
由$T=\frac{2π}{ω}=2π$,得ω=1,…(2分)
又$\left\{\begin{array}{l}{B+A=4}\\{B-A=-2}\end{array}\right.$,解得A=3,B=1 …(5分)
令$\frac{5π}{6}$+φ=2kπ+$\frac{π}{2}$,k∈Z,
得φ=2kπ-$\frac{π}{3}$,又|φ|<$\frac{π}{2}$,
可得当k=0时,φ=-$\frac{π}{3}$,
则f(x)=3sin(x-$\frac{π}{3}$)+1,…(8分)
(2)当2kπ+$\frac{π}{2}$≤x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈Z,
得2kπ+$\frac{5π}{6}$≤x≤2kπ+$\frac{11π}{6}$,k∈Z,
所以f(x)的单调递减区间为[2kπ+$\frac{5π}{6}$,2kπ+$\frac{11π}{6}$],k∈Z,…(12分)
(说明:k∈Z条件只要有一个不扣分,没有扣1分)
点评 本题主要考查三角函数的解析式的求解以及三角函数单调性的求解,根据条件求出A,ω和φ的值是解决本题的关键.

练习册系列答案
相关题目
17.甲、乙两人在一次设计比赛中各射靶5次,两人成绩的条形图如图所示,则( )
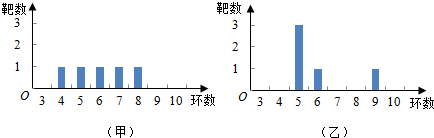

| A. | 甲的成绩的平均数小于乙的成绩的平均数 | |
| B. | 甲的成绩的极差小于乙的成绩的极差 | |
| C. | 甲的成绩的方差小于乙的成绩的方差 | |
| D. | 甲的成绩的中位数等于乙的成绩的中位数 |
14.设定义在(1,e)上的函数f(x)=$\sqrt{lnx+4x-a}$(a∈R),若曲线y=1+sinx上存在(x0,y0)使得f(f(y0))=y0,则a的取值范围( )
| A. | (-∞,4+ln2] | B. | (3,4] | C. | (3,4+ln2] | D. | (2,ln2] |