题目内容
8.在(x-$\sqrt{2}$)10(x+$\sqrt{2}$)10展开式中,x14的系数为-960.分析 计算(x-$\sqrt{2}$)10(x+$\sqrt{2}$)10=(x2-2)10,利用二项式展开式的通项Tr+1求出展开式中x14的系数即可.
解答 解:∵(x-$\sqrt{2}$)10(x+$\sqrt{2}$)10=(x2-2)10,
∴它的展开式中通项为
Tr+1=${C}_{10}^{r}$•x2(10-r)•(-2)r,
令2(10-r)=14,
解得r=3;
∴展开式中x14的系数为
${C}_{10}^{3}$•(-2)3=-960.
故答案为:-960.
点评 本题考查了二项式定理的应用问题,解题时利用二项式展开式的通项公式,是基础题目.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
17.甲、乙两人在一次设计比赛中各射靶5次,两人成绩的条形图如图所示,则( )
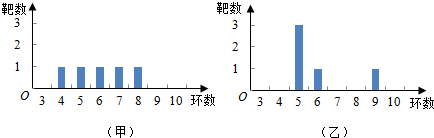

| A. | 甲的成绩的平均数小于乙的成绩的平均数 | |
| B. | 甲的成绩的极差小于乙的成绩的极差 | |
| C. | 甲的成绩的方差小于乙的成绩的方差 | |
| D. | 甲的成绩的中位数等于乙的成绩的中位数 |