题目内容
【题目】如图,在三棱锥![]() 中平面
中平面![]() 平面
平面![]() ,
,![]() .
.
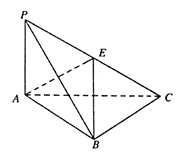
(Ⅰ)证明:![]() ;
;
(Ⅱ)若点E为![]() 中点,
中点,![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(Ⅰ)证明见解析,(Ⅱ)![]()
【解析】
(1)过B作![]() 于点D,则
于点D,则![]() 平面
平面![]() ,可得
,可得![]() ,又
,又![]() ,则
,则![]() 平面
平面![]() ,即可得证.
,即可得证.
(2)以![]() 为坐标原点,过
为坐标原点,过![]() 作垂直
作垂直![]() 的直线为
的直线为![]() 轴,
轴,![]() 为
为![]() 轴正向,
轴正向,![]() 为
为![]() 轴建立如图所以空间直角坐标系,分别求出平面
轴建立如图所以空间直角坐标系,分别求出平面![]() 、平面
、平面![]() 的法向量,利用空间向量法求出二面角的余弦值.
的法向量,利用空间向量法求出二面角的余弦值.
证明:(1)过B作![]() 于点D,
于点D,
![]() 平面
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
∴![]()
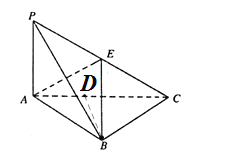
(2)由(1)有![]() 平面
平面![]() ,故以
,故以![]() 为坐标原点,过
为坐标原点,过![]() 作垂直
作垂直![]() 的直线为
的直线为![]() 轴,
轴,![]() 为
为![]() 轴正向,
轴正向,![]() 为
为![]() 轴建立如图所以空间直角坐标系
轴建立如图所以空间直角坐标系
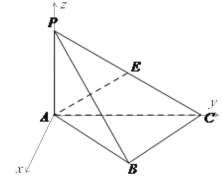
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
故![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() 则
则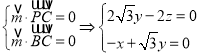 ,
,
令![]() 有
有 ,故
,故![]() ,
,
同理可得平面![]() 的法向量
的法向量![]() ,
,
则 ,又平面
,又平面![]() 与平面
与平面![]() 所成角为锐角,
所成角为锐角,
所以平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]()

练习册系列答案
相关题目
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
