Question

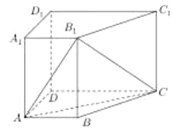
【题目】在棱长为2的正方体中，点是正方体棱上一点，.

①若，则满足条件的点的个数为______；

②若满足的点的个数为6，则的取值范围是______.

Answer 1

【答案】4

【解析】

（1）由题意可得点是以为焦距，以为长半轴的椭圆与正方体与棱的交点，可求解；

（2）利用三角形两边之和大于第三边，以及点的个数为6个时，短半轴范围，即可求解.

（1）正方体的棱长为，

是以为焦距，以为长半轴的椭圆，

在正方体的棱上，应是椭圆与正方体与棱的交点，

结合正方体的性质可得，满足条件的点为，

以及棱各有一点满足条件，

故满足条件的点的个数为；

（2），

当椭圆短半轴时，椭圆与棱,

各有一个交点，与其它棱无交点，满足题意，

当时，由（1）得不合题意.

当时，根据正方体的性质，

至多只有4个点在棱上，不合题意；

当时，椭圆与棱

各有一个交点，满足题意， ，

；

当，椭圆至多与正方体的棱有4个交点，不合题意.

综上 或.

故答案为:（1）4；（2）