Question

【题目】已知椭圆C的中心在原点，焦点在x轴上，D（0，2）为椭圆C短轴的一个端点，F为椭圆C的右焦点，线段DF的延长线与椭圆C相交于点E，且|DF|=3|EF|．

（1）求椭圆C的标准方程；

（2）设直线l与椭圆C相交于A，B两点，O为坐标原点，若直线OA与OB的斜率之积为-，求的取值范围．

Answer 1

【答案】（1）+=1（2）[-1，0）∪（0，1]．

【解析】

（1）先由条件得b，再根据条件得E坐标，代入椭圆方程解得a2（2）先设A，B两点坐标，化简条件得y1y2=x1x2，再代入化简=x1x2，联立直线方程与椭圆方程，解得x1，x2，最后根据基本不等式求最值，解得取值范围.

解：（1）设椭圆的方程为+=1，（a＞b＞0），右焦点F（c，0），

∵D（0，2）为椭圆C短轴的一个端点，

∴b=2，

∵|DF|=3|EF|，

∴E（，-），

∴+=1，即a2=2c2，

又c2=a2-4，

∴a2=2（a2-4），

解得a2=8，

故椭圆方程为+=1．

（2）∵kOAkOB=＜0，设kOA=k≠0，则kOB=，

设A（x1，y1），B（x2，y2），

∴=，

即y1y2=x1x2，

∴=x1x2+y1y2=x1x2，

由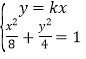，消y可得x2+2k2x2=8，即x12=，

同理x22==，

∴x12x22==≤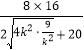==4，

当且仅当4k2=，即k=±时取等号，

∴-2≤x1x2≤2，且x1x2≠0，

∴-1≤t≤1，且t≠0，

故的取值范围为[-1，0）∪（0，1]．