题目内容
【题目】如图,已知直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上. 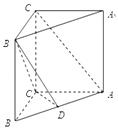
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当 ![]() =
= ![]() 时,求二面角B﹣CD﹣B1的余弦值.
时,求二面角B﹣CD﹣B1的余弦值.
【答案】
(1)证明:连接BC1,交B1C于E,连接DE.
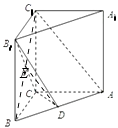
∵ABC﹣A1B1C1是直三棱柱,D是AB中点
∴侧面BB1C1C为矩形,DE为△ABC1的中位线
∴DE∥AC1,
又∵DE平面B1CD,AC1平面B1CD
∴AC1∥平面B1CD.
(2)∵AB=5,AC=4,BC=3,即AB2=AC2+BC2
∴AC⊥BC,所以如图,以C为原点建立空间直角坐标系C﹣xyz.

则B (3,0,0),A (0,4,0),
A1 (0,4,4),B1 (3,0,4).
设D (a,b,0)(a>0,b>0),
∵点D在线段AB上,且 ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
![]()
∴a= ![]() ,b=
,b= ![]()
∴ ![]() =(﹣3,0,﹣4),
=(﹣3,0,﹣4), ![]() =(
=( ![]() ,
, ![]() ,0)
,0)
显然 ![]() =(0,0,4)是平面BCD的一个法向量
=(0,0,4)是平面BCD的一个法向量
设平面B1CD的法向量为 ![]() =(x,y,z),那么
=(x,y,z),那么
由 ![]()
![]() =0,
=0, ![]()
![]() =0,得
=0,得 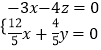 ,
,
令x=1,得 ![]() =(1,﹣3,﹣
=(1,﹣3,﹣ ![]() )
)
∴cos ![]() =
= =
![]() =﹣
=﹣ ![]()
又二面角B﹣CD﹣B1是锐角,故其余项值为 ![]()
【解析】(1)通过作平行线,由线线平行证明线面平行;(2)建立空间直角坐标系,求得两平面的法向量,利用向量法求二面角的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
