题目内容
8.设集合S={1,2,3,4,5,6,7,8,9},A={a1,a2,a3}是S的子集,且a1、a2、a3满足a1<a2<a3,a3-a2≤5,则满足条件的集合A的个数为80.分析 根据条件,可考虑用逆向的方法求解,从9个数中任取3个数组成集合,显然组成${{∁}_{9}}^{3}$中取法,而不符合条件的集合容易求出有3个,从而得出满足条件的集合A的个数为∁93-3.
解答 解:从集合S中任取3个元素,有${{∁}_{9}}^{3}$=84种取法;
而a1=1,a2=2,a3=8;a1=1,a2=2,a3=9;a1=1,a2=3,a3=9;a1=2,a2=3,a3=9这4种取法不符合条件,不能构成集合A的元素;
∴满足条件的集合A的个数为84-4=80.
故答案为:80.
点评 考查列举法表示集合,子集的概念,以及逆向思维解题的方法.

练习册系列答案
相关题目
19.已知集合M=|x|x2-2x<0|,N=|x|x>1|,则M∩∁RN=( )
| A. | [1,2) | B. | (1,2) | C. | [0,1) | D. | (0,1] |
3.设全集U=R,A={x||x|<2},B={x|y=$\sqrt{x-1}$},则图中阴影部分所表示的集合( )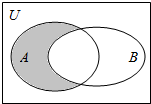

| A. | (-2,+∞) | B. | (1,2] | C. | (-2,1) | D. | (-2,1] |
13.已知集合A={x|x2-2x-3≤0},B={x|x<a},若A⊆B,则实数a的取值范围是( )
| A. | (-1,+∞) | B. | [-1,+∞) | C. | (3,+∞) | D. | [3,+∞) |
20.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁UA)∩B=( )
| A. | {2} | B. | {2,4} | C. | {0,4} | D. | {4} |