Question

【题目】在三棱锥 中，平面 平面 ， ， 分别为 的中点.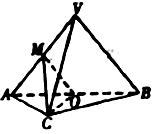

（1）求证： 平面 ；
（2）求证：平面 平面 .

Answer 1

【答案】
（1）解：因为 分别为 的中点，所以 ，
又因为 平面 ， 平面 ，所以 平面
（2）证明：因为 ， 为 的中点，所以 .
又因为平面 平面 ，平面 平面 ，且 平面 ，
所以 平面 ，又 平面 ，所以平面 平面
【解析】（1）利用三角形中位线得到 O M / / V B，再用线面平行的判定定理证得 V B / / 平面 M O C 。
（2）由面面垂直的性质定理得到O C ⊥ 平面 V A B，再用面面垂直判定定理证得。
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识，掌握一个平面过另一个平面的垂线，则这两个平面垂直．