题目内容
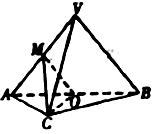
【题目】如图,在三棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() 在
在 ![]() ,且
,且 ![]() .
.
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)在线段 ![]() 上是否存在点
上是否存在点 ![]() ,使二面角
,使二面角 ![]() 的大小为
的大小为 ![]() ?若存在,求出
?若存在,求出 ![]() 的长;
的长;
若不存在,请说明理由.
【答案】
(1)证明:由 ![]() ,
,![]() 是
是 ![]() 的中点,得
的中点,得 ![]() ,
,
因为 ![]() 底面
底面 ![]() ,所以
,所以 ![]() ,
,
在 ![]() 中,
中, ![]() ,所以
,所以 ![]() ,
,
因此 ![]() ,又因为
,又因为 ![]() ,
,
所以 ![]() ,
,
则 ![]() ,即
,即 ![]() ,因为
,因为 ![]() 底面
底面 ![]() ,
,
所以 ![]() ,又
,又 ![]() ,
,
又 ![]() ,所以
,所以 ![]() 平面
平面 ![]() .
.
(2)解:假设满足条件的点 ![]() ,存在,
,存在,
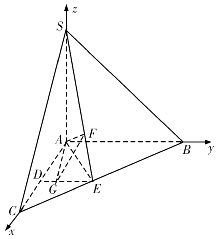
并设 ![]() ,以
,以 ![]() 为坐标原点,分别以
为坐标原点,分别以 ![]() 为
为 ![]() 轴建立空间之间坐标系
轴建立空间之间坐标系 ![]() ,
,
则 ![]() ,
,
由 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() ,
,
设平面 ![]() 的法向量为
的法向量为 ![]() ,
,
则  ,取
,取 ![]() ,得
,得 ![]() ,
,
即 ![]() ,设平面
,设平面 ![]() 的法向量为
的法向量为 ![]() ,
,
则 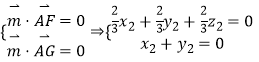 ,取
,取 ![]() ,得
,得 ![]() ,
,
即 ![]() ,
,
由二面角 ![]() 的大小为
的大小为 ![]() ,得
,得 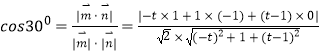 ,
,
化简得 ![]() ,又
,又 ![]() ,求得
,求得 ![]() ,于是满足条件的点
,于是满足条件的点 ![]() 存在,且
存在,且 ![]() .
.
【解析】(1)根据题意由线面垂直的性质定理即可得到线线垂直,再由已知的线线垂直结合线面垂直的判定定理即可得证。(2)根据题意结合已知条件根据题意建立空间直角坐标系,求出各个点的坐标进而求出各个向量的坐标,设出平面AFG和平面AEF的法向量,由向量垂直的坐标运算公式可求出法向量,再利用向量的数量积运算公式求出余弦值进而得到t的值于是满足条件的点 G 存在。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目