题目内容
【题目】已知函数![]() .
.
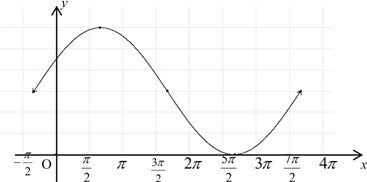
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出![]() 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由![]() 的图象经怎样的变换得到.
的图象经怎样的变换得到.

【答案】(1)见解析(2)见解析(3)见解析
【解析】分析:(1)先根据配角公式化函数为基本三角函数形式,列表,求点坐标,描点连线即得图像,(2)根据图像或正弦函数性质求![]() 的周期、振幅、初相、对称轴;(3)根据解析式关系,通过上下左右平移,以及伸缩变换得结果.注意平移单位是相对x而言.
的周期、振幅、初相、对称轴;(3)根据解析式关系,通过上下左右平移,以及伸缩变换得结果.注意平移单位是相对x而言.
详解:
解:(1)![]() =3sin(
=3sin(![]() )+3
)+3
列表
x |
|
|
|
|
|
| 0 |
|
|
|
|
| 3 | 6 | 3 | 0 | 3 |
描点作图
(2)周期T=![]() ,振幅A=3,初相
,振幅A=3,初相![]() ,
,
由![]() ,得
,得![]() 即为对称轴;
即为对称轴;
(3)①由![]() 的图象上各点向左平移
的图象上各点向左平移![]() 个长度单位,得
个长度单位,得![]() 的图象;
的图象;
②由![]() 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得
的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得![]() 的图象;
的图象;
③由![]() 的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得
的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得![]() 的图象;
的图象;
④由![]() 的图象上各点向上平移3个长度单位,得
的图象上各点向上平移3个长度单位,得![]() +3的图象.
+3的图象.

练习册系列答案
相关题目
【题目】某种商品在30天内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段![]() ,
,![]() (不包含
(不包含![]() ,
,![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.
第 | 5 | 1 5 | 2 0 | 3 0 |
销售量 | 3 5 | 2 5 | 2 0 | 1 0 |
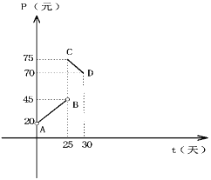
(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)