题目内容
若函数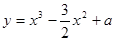 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
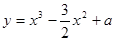 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________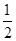
试题分析:求导得
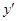 =
= ,当-1<
,当-1<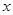 <0时,
<0时,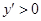 ,当
,当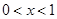 时,
时,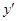 <0,所以该函数在(-1,0)上是增函数,在(0,1)是减函数,故当
<0,所以该函数在(-1,0)上是增函数,在(0,1)是减函数,故当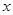 =0时,
=0时,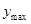 =
=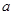 ,所以
,所以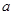 =3,所以当
=3,所以当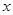 =-1时,y=
=-1时,y=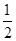 ,当
,当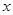 =1时,
=1时,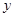 =
=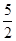 ,所以该函数在[-1,1]上的最小值为
,所以该函数在[-1,1]上的最小值为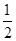 .
.
练习册系列答案
相关题目
题目内容
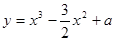 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________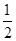
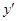 =
= ,当-1<
,当-1<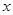 <0时,
<0时,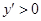 ,当
,当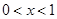 时,
时,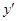 <0,所以该函数在(-1,0)上是增函数,在(0,1)是减函数,故当
<0,所以该函数在(-1,0)上是增函数,在(0,1)是减函数,故当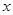 =0时,
=0时,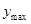 =
=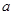 ,所以
,所以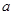 =3,所以当
=3,所以当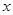 =-1时,y=
=-1时,y=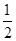 ,当
,当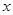 =1时,
=1时,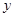 =
=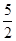 ,所以该函数在[-1,1]上的最小值为
,所以该函数在[-1,1]上的最小值为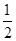 .
.