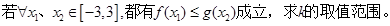题目内容
(1)讨论函数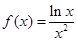 (
(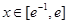 )的图像与直线
)的图像与直线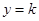 的交点个数.
的交点个数.
(2)求证:对任意的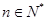 ,不等式
,不等式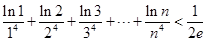 总成立.
总成立.
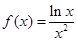 (
(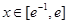 )的图像与直线
)的图像与直线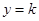 的交点个数.
的交点个数. (2)求证:对任意的
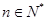 ,不等式
,不等式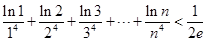 总成立.
总成立.(1)解:由题意得: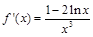 .令
.令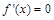 ,得
,得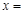
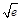 .
.
当 时,
时,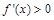 ,故函数
,故函数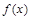 在
在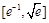 上递增;
上递增;
当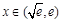 时,
时,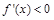 ,故函数
,故函数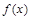 在
在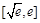 上递减;
上递减;
又因为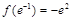 ,
,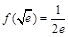 ,
,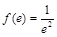 ,所以当
,所以当 或
或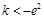 时,没有交点;当
时,没有交点;当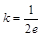 或
或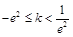 时,有唯一的交点;当
时,有唯一的交点;当 时,有两个交点.
时,有两个交点.
(2)证明:由(1)知函数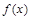 在
在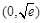 上递增,在
上递增,在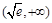 上递减,故
上递减,故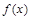 在
在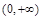 上的最大值为
上的最大值为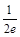 .即对
.即对 均有
均有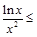
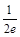 ,故
,故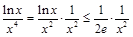 .
.
当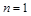 时,结论显然成立;当
时,结论显然成立;当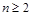 时,有:
时,有:
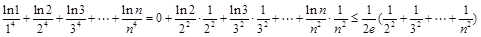
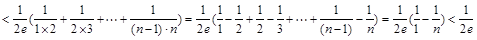 .
.
综上可知,对任意的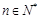 ,不等式
,不等式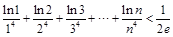 成立.
成立.
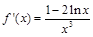 .令
.令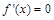 ,得
,得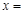
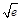 .
.当
 时,
时,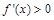 ,故函数
,故函数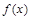 在
在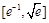 上递增;
上递增;当
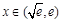 时,
时,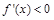 ,故函数
,故函数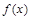 在
在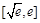 上递减;
上递减;又因为
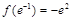 ,
,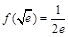 ,
,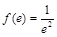 ,所以当
,所以当 或
或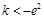 时,没有交点;当
时,没有交点;当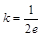 或
或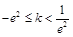 时,有唯一的交点;当
时,有唯一的交点;当 时,有两个交点.
时,有两个交点.(2)证明:由(1)知函数
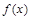 在
在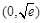 上递增,在
上递增,在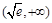 上递减,故
上递减,故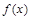 在
在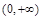 上的最大值为
上的最大值为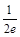 .即对
.即对 均有
均有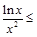
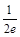 ,故
,故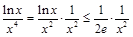 .
.当
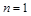 时,结论显然成立;当
时,结论显然成立;当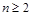 时,有:
时,有: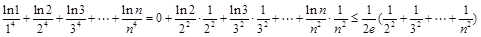
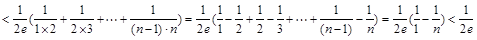 .
.综上可知,对任意的
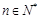 ,不等式
,不等式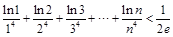 成立.
成立.本试题主要考查了运用导数的知识来解决图像与图像的交点问题,以及运用构造函数,结合导数来证明不等式的综合试题。解决该试题的关键是对于不等式证明,要用到一问中的结论,来进行放缩得证。

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 从点
从点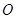 出发,按逆时针方向沿周长为
出发,按逆时针方向沿周长为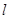 的图形运动一周,
的图形运动一周,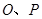 两点连线的距离
两点连线的距离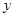 与点
与点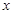 的函数关系如图,那么点
的函数关系如图,那么点
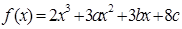 在
在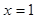 及
及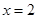 时取得极值.
时取得极值.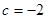 时,求函数
时,求函数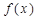 在区间
在区间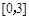 上的最大值.
上的最大值. 的图像如左图所示,那么函数
的图像如左图所示,那么函数 的图像最有可能的是( )
的图像最有可能的是( )
 的图像过坐标原点
的图像过坐标原点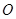 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
. ,
, 的值
的值 在区间
在区间 上的值域
上的值域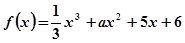 在区间
在区间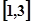 上单调函数,则实数
上单调函数,则实数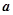 的取值范围为( ▲ )
的取值范围为( ▲ )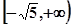

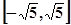
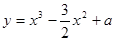 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________ .
. 极值;
极值;