题目内容
已知函数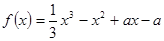 (
(
 R).
R).
(1)当 时,求函数
时,求函数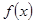 的极值;
的极值;
(2)若函数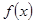 的图象与
的图象与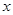 轴有且只有一个交点,求
轴有且只有一个交点,求 的取值范围.
的取值范围.
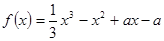 (
(
 R).
R).(1)当
 时,求函数
时,求函数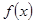 的极值;
的极值;(2)若函数
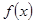 的图象与
的图象与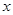 轴有且只有一个交点,求
轴有且只有一个交点,求 的取值范围.
的取值范围. (1)当 时,
时, 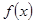 取得极大值为
取得极大值为
 ;
;
当 时,
时, 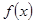 取得极小值为
取得极小值为
 .
.
(2)a的取值范围是 .
.
 时,
时, 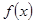 取得极大值为
取得极大值为
 ;
;当
 时,
时, 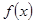 取得极小值为
取得极小值为
 .
. (2)a的取值范围是
 .
. 试题分析:(1)遵循“求导数,求驻点,讨论驻点两侧导数值符号,确定极值”.
(2) 根据
 =
= 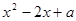 ,得到△=
,得到△=  =
=  .
.据此讨论:① 若a≥1,则△≤0,
此时
 ≥0在R上恒成立,f(x)在R上单调递增 .
≥0在R上恒成立,f(x)在R上单调递增 .计算f(0)
 ,
, ,得到结论.
,得到结论.② 若a<1,则△>0,
 = 0有两个不相等的实数根,不妨设为
= 0有两个不相等的实数根,不妨设为 .
.有
 .
. 给出当
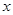 变化时,
变化时, 的取值情况表.
的取值情况表.根据f(x1)·f(x2)>0, 解得a>
 .作出结论.
.作出结论.试题解析: (1)当
 时,
时,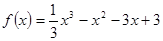 ,
,∴

 .
. 令
 ="0," 得
="0," 得  . 2分
. 2分当
 时,
时,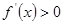 , 则
, 则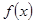 在
在 上单调递增;
上单调递增;当
 时,
时, , 则
, 则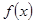 在
在 上单调递减;
上单调递减;当
 时,
时,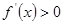 ,
, 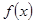 在
在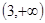 上单调递增. 4分
上单调递增. 4分 ∴ 当
 时,
时, 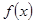 取得极大值为
取得极大值为
 ;
;当
 时,
时, 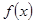 取得极小值为
取得极小值为
 . 6分
. 6分 (2) ∵
 =
= 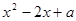 ,
,∴△=
 =
=  .
. ①若a≥1,则△≤0, 7分
∴
 ≥0在R上恒成立,
≥0在R上恒成立,∴ f(x)在R上单调递增 .
∵f(0)
 ,
, ,
, ∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. 9分
② 若a<1,则△>0,
∴
 = 0有两个不相等的实数根,不妨设为
= 0有两个不相等的实数根,不妨设为 .
.∴
 .
. 当
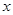 变化时,
变化时, 的取值情况如下表:
的取值情况如下表: | x |  | x1 | (x1,x2) | x2 |  |
 | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∵
 ,
,∴
 .
.∴

=
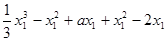

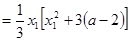 .
.同理

 .
.∴



 .
.令f(x1)·f(x2)>0, 解得a>
 .
.而当
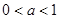 时,
时, , 13分
, 13分故当
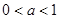 时, 函数f(x)的图象与x轴有且只有一个交点.
时, 函数f(x)的图象与x轴有且只有一个交点.综上所述,a的取值范围是
 . 14分
. 14分
练习册系列答案
相关题目
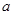 是实数,函数
是实数,函数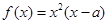 .
.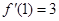 ,求
,求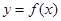 在点
在点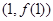 处的切线方程.
处的切线方程.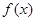 在
在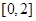 上的最大值.
上的最大值.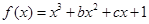 有两个极值点
有两个极值点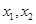 且
且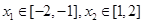 ,则
,则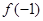 的取值范围是( )
的取值范围是( )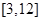
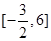
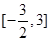
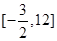
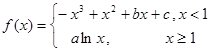 的图像过坐标原点
的图像过坐标原点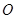 ,且在点
,且在点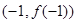 处的切线的斜率是
处的切线的斜率是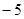 .
.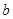 ,
, 的值
的值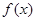 在区间
在区间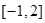 上的值域
上的值域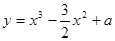 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________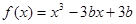 在(0,1)内有极小值,则 ( )
在(0,1)内有极小值,则 ( )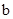 <1
<1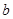 <1
<1
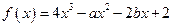 处有极值,则ab的最大值等于( ).
处有极值,则ab的最大值等于( ).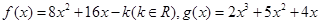 .
.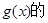 极值;
极值;