题目内容
已知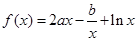 在
在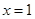 与
与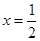 处都取得极值.
处都取得极值.
(1)求 ,
,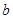 的值;
的值;
(2)设函数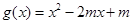 ,若对任意的
,若对任意的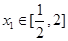 ,总存在
,总存在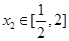 ,使得:
,使得: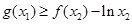 ,求实数
,求实数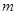 的取值范围.
的取值范围.
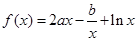 在
在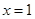 与
与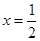 处都取得极值.
处都取得极值. (1)求
 ,
,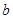 的值;
的值;(2)设函数
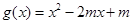 ,若对任意的
,若对任意的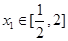 ,总存在
,总存在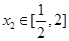 ,使得:
,使得: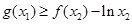 ,求实数
,求实数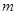 的取值范围.
的取值范围.(1)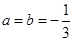 ;(2)
;(2)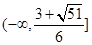 .
.
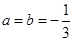 ;(2)
;(2)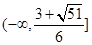 .
.试题分析:(1)根据条件
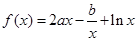 ,可得
,可得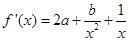 ,由
,由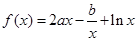 在
在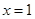 与
与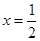 处都取得极值,可知
处都取得极值,可知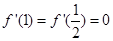 ,故可建立关于
,故可建立关于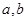 的二元一次方程组,从而解得
的二元一次方程组,从而解得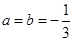 ,此时,需要代回检验
,此时,需要代回检验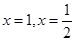 是否确实是
是否确实是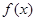 的极值点,经检验
的极值点,经检验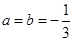 符合题意,从而
符合题意,从而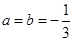 ;(2)由(1)可得由(1)知:函数
;(2)由(1)可得由(1)知:函数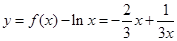 在
在 上递减,
上递减,∴
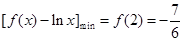 ,因此问题就等价于求使当
,因此问题就等价于求使当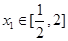 时,
时,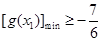 恒成立的
恒成立的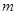 的取值范围,而二次函数
的取值范围,而二次函数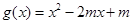 图像的对称轴是
图像的对称轴是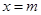 ,因此需对
,因此需对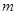 的取值作出以下三种情况的分类讨论:①:
的取值作出以下三种情况的分类讨论:①: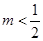 ;②:
;②: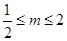 ;③
;③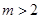 ,分别用含
,分别用含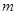 的代数式表示上述三种情况下
的代数式表示上述三种情况下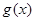 的最小值表示出来,从而可以建立关于
的最小值表示出来,从而可以建立关于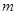 的不等式,进而求得
的不等式,进而求得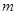 的取值范围为
的取值范围为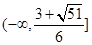 .
.试题解析:(1)∵
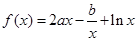 ,∴
,∴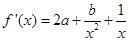 1分
1分∵
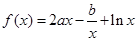 在
在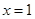 与
与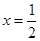 处都取得极值,
处都取得极值,∴
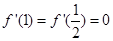 ,∴
,∴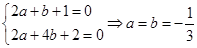 4分
4分经检验,当
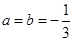 时,
时,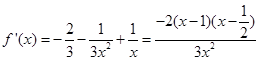 ,
,∴函数
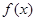 在
在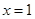 与
与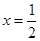 处都取得极值,∴
处都取得极值,∴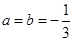 6分;
6分; (2)由(1)知:函数
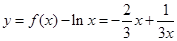 在
在 上递减,
上递减,∴
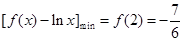 8分
8分又 ∵函数
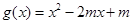 图象的对称轴是
图象的对称轴是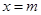 ,
,①:当
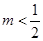 时:
时: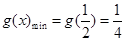 ,显然有
,显然有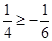 成立, ∴
成立, ∴ 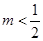 ,
,②:当
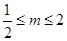 时:
时: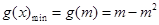 ,∴
,∴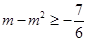 , 解得:
, 解得: ,
,又∵
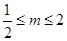 ,∴
,∴ .
.③:当
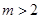 时:
时: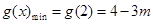 ,∴
,∴ 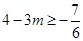 , ∴
, ∴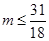 , 又
, 又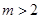 ,∴
,∴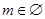
综上所述:
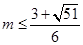 12分,
12分,∴实数
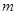 的取值范围为
的取值范围为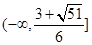 13分.
13分.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
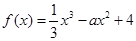 ,且
,且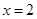 是函数
是函数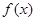 的一个极小值点.
的一个极小值点.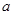 的值;
的值;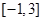 上的最大值和最小值.
上的最大值和最小值.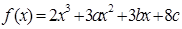 在
在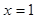 及
及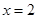 时取得极值.
时取得极值.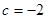 时,求函数
时,求函数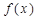 在区间
在区间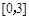 上的最大值.
上的最大值.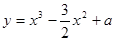 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________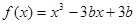 在(0,1)内有极小值,则 ( )
在(0,1)内有极小值,则 ( )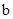 <1
<1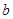 <1
<1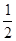
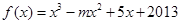 在
在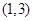 上只有一个极值点,则实数
上只有一个极值点,则实数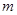 的取值范围为 .
的取值范围为 . .
. 极值;
极值;