题目内容
9.设x,y满足约束条件$\left\{{\begin{array}{l}{x-y≤0}\\{x+y-1≥0}\\{x-2y+2≥0}\end{array}}$,则z=x+3y+m的最大值为4,则m的值为-4.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,结合z=x+3y+m的最大值为4,建立解关系即可求解m的值.
解答 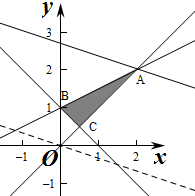 解:由z=x+3y+m得$y=-\frac{1}{3}x+\frac{z}{3}$-$\frac{m}{3}$,
解:由z=x+3y+m得$y=-\frac{1}{3}x+\frac{z}{3}$-$\frac{m}{3}$,
作出不等式组对应的平面区域如图(阴影部分):
平移直线$y=-\frac{1}{3}x+\frac{z}{3}$-$\frac{m}{3}$由图象可知当直线$y=-\frac{1}{3}x+\frac{z}{3}$-$\frac{m}{3}$经过点A时,直线$y=-\frac{1}{3}x+\frac{z}{3}$-$\frac{m}{3}$的截距最大,
此时z也最大,由$\left\{\begin{array}{l}{x-y=0}\\{x-2y+2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即A(2,2),
将A代入目标函数z=x+3y+m,得2+3×2+m=4.
解得m=-4,
故答案为:-4.
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图是正方体的平面展开图,则在这个正方体中,求证:DE∥平面BCM.
如图是正方体的平面展开图,则在这个正方体中,求证:DE∥平面BCM.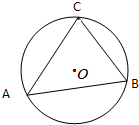 如图,已知⊙O是△ABC的外接圆,直径为2R,试用R与∠A、∠B、∠C的三角比来表示三角形的三条边长.
如图,已知⊙O是△ABC的外接圆,直径为2R,试用R与∠A、∠B、∠C的三角比来表示三角形的三条边长.