题目内容
4．求（1-2x）5（1+3x）4展开式中按x的升幂排列的第3项．分析 （1-2x）5（1+3x）4的展开式中按x的升幂排列的第3项，即展开式中含x2的项．
解答 解：（1-2x）5（1+3x）4的展开式中按x的升幂排列的第3项，即展开式中含x2的项，
${C}_{4}^{2}•（3x）^{2}$+${C}_{5}^{2}$（-2x）2+${C}_{5}^{1}•（-2x）•{C}_{4}^{1}•3x$=-26x2．
点评 本题主要考查二项式定理，二项展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
12．设等比数列{an}的首项a1=$\frac{1}{3}$，前n项和为Sn，若S1、2S2、3S3成等差数列，则{an}的通项为（ ）
| A． | an=$\frac{1}{{3}^{n}}$ | B． | an=3n | C． | an=$\frac{1}{{3}^{n-1}}$ | D． | an=$\frac{1}{{3}^{1-n}}$ |
19．已知抛物线方程为y=4x2，则该抛物线的焦点坐标为（ ）
| A． | （0，1） | B． | $（0，\frac{1}{16}）$ | C． | （1，0） | D． | $（\frac{1}{16}，0）$ |
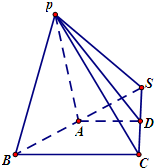在三棱锥P-SBC中，A，D分别为边SB，SC的中点，AB=2，BC=4，CD=2$\sqrt{2}$．平面PSB⊥平面ABCD，平面PAD⊥平面ABCD．