题目内容

18．如图，已知⊙O是△ABC的外接圆，直径为2R，试用R与∠A、∠B、∠C的三角比来表示三角形的三条边长．

分析 连接CO并延长，与圆O交于点D，连接BD，利用圆周角定理得到∠D=∠A，∠CBD=90°，在直角三角形BCD中，利用锐角三角函数定义表示出BC，即为a，同理表示出b与c即可．

解答 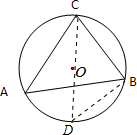解：连接CO并延长，与圆O交于点D，连接BD，
可得∠D=∠A，∠CBD=90°，
在Rt△BCD中，CD=2R，sinD=sinA，
∴BC=a=2RsinA，
同理得到AB=2RsinC，AC=2RsinB．

点评 此题考查了正弦定理，圆周角定理，以及锐角三角函数定义，熟练掌握正弦定理是解本题的关键．

练习册系列答案
相关题目
8．函数y=sinx，x∈[π，2π]的值域是（　　）
A．[-1，1]B．[0，1]C．[-1，0]D．[0，$\frac{1}{2}$]
9．设x，y满足约束条件$\left\{{\begin{array}{l}{x-y≤0}\\{x+y-1≥0}\\{x-2y+2≥0}\end{array}}$，则z=x+3y+m的最大值为4，则m的值为-4．
6．给出下列四个命题：
①△ABC中，A＞B是sinA＞sinB成立的充要条件；
②当x＞0且x≠1时，有$lnx+\frac{1}{lnx}≥2$；
③已知Sn是等差数列{an}的前n项和，若S7＞S5，则S9＞S3；
④若函数$y=f（x-\frac{3}{2}）$为R上的奇函数，则函数y=f（x）的图象一定关于点F（$\frac{3}{2}$，0）成中心对称．
其中所有正确命题的序号为①③．
13．在（1-2x3）（1+x）5的展开式中，x4系数为-5．
3．△ABC中，点M在线段AC上，点P在线段BM上，且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2，若$|{\overrightarrow{AB}}|=2，|{\overrightarrow{AC}}|=3，∠BAC={90°}$，则$\overrightarrow{AP}•\overrightarrow{BC}$的值为$-\frac{2}{3}$．
10．若a＞1，b＜1，则下列两式的大小关系为ab+1＜a+b．
7．“a=-l”是“直线（a-1）x-y-l=0与直线2x-ay+l=0平行”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
8．若sinαcosα＜0，sinαtanα＜0，化简$\sqrt{\frac{1-sin\frac{α}{2}}{1+sin\frac{α}{2}}}$+$\sqrt{\frac{1+sin\frac{α}{2}}{1-sin\frac{α}{2}}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网