Question

【题目】如图，在四边形ACBD中， ，且△ABC为正三角形．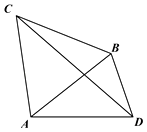

（Ⅰ）求cos∠BAD的值；
（Ⅱ）若CD=4， ，求AB和AD的长．

Answer 1

【答案】解：（Ⅰ）因为 ，∠CAD∈（0，π）

所以

所以cos∠BAD= = = =

（Ⅱ）设AB=AC=BC=x，AD=y，在△ACD和△ABD中由余弦定理得

代入得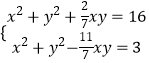

解得 或 （舍）

即 ，

【解析】（Ⅰ）根据sin2+cos2=1可得出sin，又因为=，根据两角差的余弦公式cos(）=coscos+sinsin展开；（Ⅱ）根据余弦定理a2=b2+c2-2bccosA列出关于AB与AD的方程，联立组成方程组即可求解.
【考点精析】关于本题考查的两角和与差的余弦公式，需要了解两角和与差的余弦公式：才能得出正确答案．