Question

【题目】若存在过点（1，0）的直线与曲线y=x3和 都相切，则a等于（ ）
A.﹣1或
B.﹣1或
C. 或
D. 或7

Answer 1

【答案】A
【解析】解：由y=x3y'=3x2 ， 设曲线y=x3上任意一点（x0 ， x03）处的切线方程为y﹣x03=3x02（x﹣x0），（1，0）代入方程得x0=0或 ①当x0=0时，切线方程为y=0，此直线是y=x3的切线，故 仅有一解，由△=0，解得a=﹣
②当 时，切线方程为 ，由 ，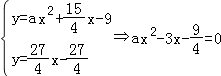
∴a=﹣1或a=﹣ ．
故选A
【考点精析】根据题目的已知条件，利用导数的几何意义的相关知识可以得到问题的答案，需要掌握通过图像,我们可以看出当点趋近于时，直线与曲线相切．容易知道，割线的斜率是，当点趋近于时，函数在处的导数就是切线PT的斜率k，即．