题目内容
【题目】已知椭圆C1: ![]() 的离心率为
的离心率为 ![]() ,且经过点M
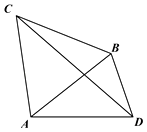
,且经过点M ![]() 的直径C1的长轴.如图,C是椭圆短轴端点,动直线AB过点C且与圆C2交于A,B两点,CD垂直于AB交椭圆于点D.
的直径C1的长轴.如图,C是椭圆短轴端点,动直线AB过点C且与圆C2交于A,B两点,CD垂直于AB交椭圆于点D. 
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值,并求此时直线AB的方程.
【答案】
(1)解:∵椭圆C1: ![]() 的离心率为
的离心率为 ![]() ,
,
∴ ![]() ,∴a=2k,b=k,k>0,
,∴a=2k,b=k,k>0,
∴ ![]() ,
,
∵椭圆C1经过点M ![]()
![]() ,
, ![]() ),
),
∴ ![]() ,解得k2=1,
,解得k2=1,
∴椭圆C1的方程为 ![]() .
.
(2)解:设A(x1,y1),B(x2,y2),D(x0,y0),
由题意知直线l1的斜率存在,设直线l1的方程为y=kx+1,
又圆C2:x2+y2=4,
∴点O到直线l1的距离d= ![]() ,
,
∴|AB|=2 ![]() =2
=2 ![]() ,
,
又∵l1⊥l2,∴直线l2的方程为x+ky﹣k=0.
由  ,消去y,得:
,消去y,得:
(4+k2)x2+8kx=0,
∴ ![]() ,
,
∴|CD|= ![]() ,
,
设△ABD的面积为S,则S= ![]() =
= ![]() ,
,
∴S= ![]()
≤  =
= ![]() ,
,
当且仅当k= ![]() 时取等号,
时取等号,
∴所求的直线l1的方程为 ![]() .
.
【解析】(1)由已知条件得 ![]() ,所以设椭圆方程为
,所以设椭圆方程为 ![]() ,再由椭圆C1经过点M
,再由椭圆C1经过点M ![]()
![]() ,
, ![]() ),能求出椭圆C1的方程.(2)设A(x1 , y1),B(x2 , y2),D(x0 , y0),设直线l1的方程为y=kx+1,又圆C2:x2+y2=4,求出点O到直线l1的距离和|AB|,求出直线l2的方程为x+ky﹣k=0.由此能求出直线l1的方程.
),能求出椭圆C1的方程.(2)设A(x1 , y1),B(x2 , y2),D(x0 , y0),设直线l1的方程为y=kx+1,又圆C2:x2+y2=4,求出点O到直线l1的距离和|AB|,求出直线l2的方程为x+ky﹣k=0.由此能求出直线l1的方程.

练习册系列答案
相关题目