题目内容
已知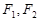 分别为椭圆
分别为椭圆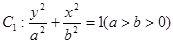 的上下焦点,其中
的上下焦点,其中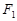 也是抛物线
也是抛物线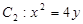 的焦点,点
的焦点,点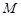 是
是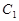 与
与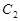 在第二象限的交点,且
在第二象限的交点,且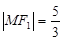 .
.
(1) 求椭圆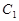 的方程;(5分)
的方程;(5分)
(2) 已知点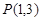 和圆
和圆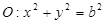 ,过点
,过点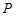 的动直线
的动直线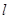 与圆
与圆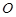 相交于不同的两
相交于不同的两
点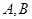 ,在线段
,在线段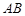 上取一点
上取一点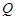 ,满足
,满足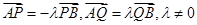 且
且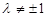 .
.
求证:点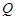 总在某定直线上.(7分)
总在某定直线上.(7分)
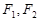 分别为椭圆
分别为椭圆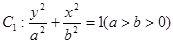 的上下焦点,其中
的上下焦点,其中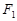 也是抛物线
也是抛物线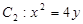 的焦点,点
的焦点,点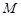 是
是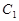 与
与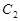 在第二象限的交点,且
在第二象限的交点,且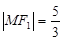 .
.(1) 求椭圆
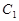 的方程;(5分)
的方程;(5分)(2) 已知点
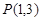 和圆
和圆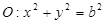 ,过点
,过点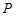 的动直线
的动直线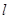 与圆
与圆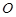 相交于不同的两
相交于不同的两点
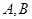 ,在线段
,在线段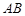 上取一点
上取一点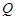 ,满足
,满足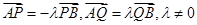 且
且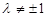 .
.求证:点
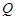 总在某定直线上.(7分)
总在某定直线上.(7分)(1)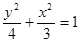 (2)见解析
(2)见解析
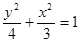 (2)见解析
(2)见解析 (I)根据抛物线的焦点坐标可求出c值,然后利用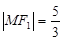 和抛物线的焦半径公式求出点M的坐标,根据点M在椭圆上,建立方程可求出椭圆的标准方程.
和抛物线的焦半径公式求出点M的坐标,根据点M在椭圆上,建立方程可求出椭圆的标准方程.
(3) 证明点Q总在一条直线上,就是证明点Q的坐标总是满足某条直线方程,设 ,由
,由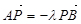 和
和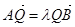 可得四个方程,然后再结合点A、B都在圆上,对四个方程进行变形求解
可得四个方程,然后再结合点A、B都在圆上,对四个方程进行变形求解
(1)由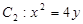 知,
知,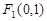 ,设
,设 ,因
,因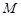 在抛物线
在抛物线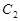 上,故
上,故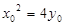 ,又
,又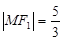 ,则
,则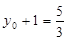 ,得
,得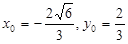 ,而点
,而点
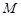 在椭圆上,有
在椭圆上,有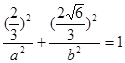 ,又
,又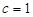 ,所以椭圆方程为
,所以椭圆方程为 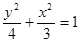 (5分)
(5分)
(2)设 ,由
,由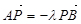 ,得
,得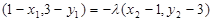 ,即
,即 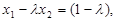 ①
① 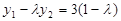 ②
②
由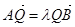 ,得
,得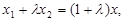 ③
③ 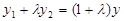 , ④ -------- (7分)
, ④ -------- (7分)
 ①
① ③,得
③,得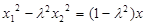 , ②
, ② ④,得
④,得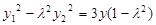 -----(9分)
-----(9分)
两式相加得 ,又点
,又点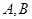 在圆
在圆
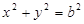 上,由(1)知,即在圆
上,由(1)知,即在圆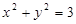 上,且
上,且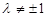 ,
,
(4)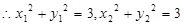 ,即
,即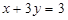 ,
,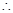 点
点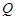 总在定直线
总在定直线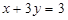 上
上
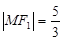 和抛物线的焦半径公式求出点M的坐标,根据点M在椭圆上,建立方程可求出椭圆的标准方程.
和抛物线的焦半径公式求出点M的坐标,根据点M在椭圆上,建立方程可求出椭圆的标准方程.(3) 证明点Q总在一条直线上,就是证明点Q的坐标总是满足某条直线方程,设
 ,由
,由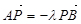 和
和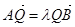 可得四个方程,然后再结合点A、B都在圆上,对四个方程进行变形求解
可得四个方程,然后再结合点A、B都在圆上,对四个方程进行变形求解(1)由
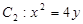 知,
知,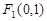 ,设
,设 ,因
,因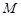 在抛物线
在抛物线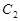 上,故
上,故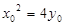 ,又
,又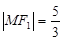 ,则
,则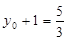 ,得
,得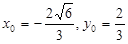 ,而点
,而点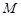 在椭圆上,有
在椭圆上,有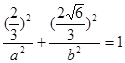 ,又
,又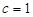 ,所以椭圆方程为
,所以椭圆方程为 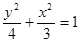 (5分)
(5分)(2)设
 ,由
,由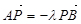 ,得
,得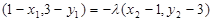 ,即
,即 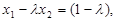 ①
① 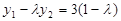 ②
②由
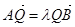 ,得
,得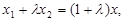 ③
③ 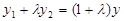 , ④ -------- (7分)
, ④ -------- (7分)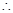 ①
① ③,得
③,得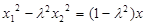 , ②
, ② ④,得
④,得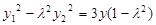 -----(9分)
-----(9分)两式相加得
 ,又点
,又点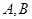 在圆
在圆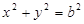 上,由(1)知,即在圆
上,由(1)知,即在圆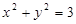 上,且
上,且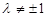 ,
,(4)
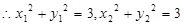 ,即
,即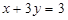 ,
,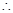 点
点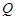 总在定直线
总在定直线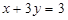 上
上
练习册系列答案
相关题目
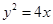 的焦点F,直线l过点
的焦点F,直线l过点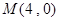 。
。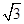 ,求直线l的斜率;
,求直线l的斜率;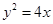 的焦点
的焦点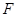 的直线交抛物线于
的直线交抛物线于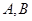 两点,点
两点,点 是原点,若
是原点,若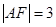 ,则
,则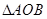 的面积为( )
的面积为( )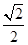
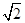
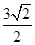
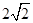
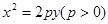 的焦点作斜率为1的直线与该抛物线交于A、B两点,A、B在
的焦点作斜率为1的直线与该抛物线交于A、B两点,A、B在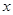 轴上的正射影分别为D、C。若梯形ABCD的面积为
轴上的正射影分别为D、C。若梯形ABCD的面积为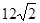 ,则
,则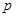 = 。
= 。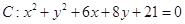 ,抛物线
,抛物线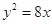 的准线为
的准线为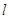 ,设抛物线上任意一点
,设抛物线上任意一点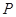 到直线
到直线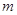 ,则
,则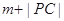 的最小值为
的最小值为 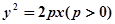 的所有焦点弦中,弦长的最小值为( )
的所有焦点弦中,弦长的最小值为( )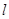 与抛物线
与抛物线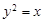 交于
交于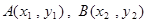 两点,与
两点,与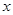 轴相交于点
轴相交于点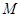 ,且
,且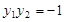 .
.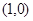 ;
;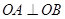 ;
;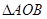 的面积的最小值.
的面积的最小值.
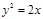 与过焦点的直线l交于A、B两点,则
与过焦点的直线l交于A、B两点,则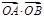 等于( ).
等于( ).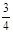 B.
B. 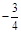 C. 3 D. -2
C. 3 D. -2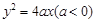 的焦点坐标是( )
的焦点坐标是( )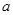 , 0)
, 0)