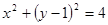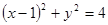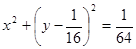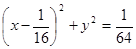题目内容
(14分)已知抛物线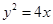 的焦点F,直线l过点
的焦点F,直线l过点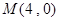 。
。
(1)若点F到直线l的距离为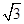 ,求直线l的斜率;
,求直线l的斜率;
(2)设A,B为抛物线上两点,且AB不与x轴垂直,若线段AB的垂直平分线恰过点M,求证:线段AB中点的横坐标为定值。
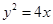 的焦点F,直线l过点
的焦点F,直线l过点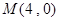 。
。(1)若点F到直线l的距离为
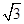 ,求直线l的斜率;
,求直线l的斜率;(2)设A,B为抛物线上两点,且AB不与x轴垂直,若线段AB的垂直平分线恰过点M,求证:线段AB中点的横坐标为定值。
(1)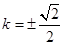 ;(2)见解析
;(2)见解析
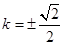 ;(2)见解析
;(2)见解析本试题主要是考查了抛物线的方程与性质的运用,以及点到直线的距离公式的求解,以及直线与抛物线位置关系的综合运用。
(1)设直线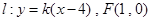
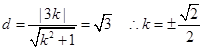
(2)设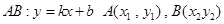
由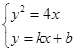 得
得 结合韦达定理得到AB的中点,然后利用斜率关系得到结果。
结合韦达定理得到AB的中点,然后利用斜率关系得到结果。
解:(1)设直线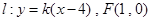
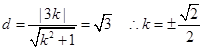 ……(4分)
……(4分)
(2)设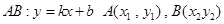
由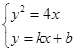 得
得
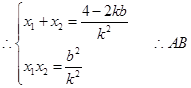 中点
中点
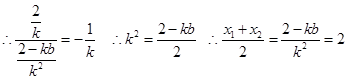 ……(14分)
……(14分)
(1)设直线
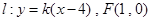
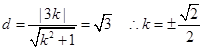
(2)设
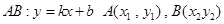
由
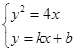 得
得 结合韦达定理得到AB的中点,然后利用斜率关系得到结果。
结合韦达定理得到AB的中点,然后利用斜率关系得到结果。解:(1)设直线
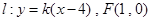
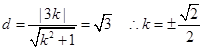 ……(4分)
……(4分)(2)设
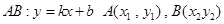
由
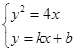 得
得
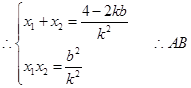 中点
中点
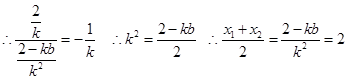 ……(14分)
……(14分)
练习册系列答案
相关题目
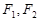 分别为椭圆
分别为椭圆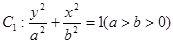 的上下焦点,其中
的上下焦点,其中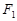 也是抛物线
也是抛物线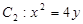 的焦点,点
的焦点,点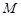 是
是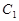 与
与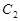 在第二象限的交点,且
在第二象限的交点,且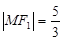 .
.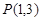 和圆
和圆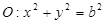 ,过点
,过点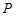 的动直线
的动直线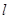 与圆
与圆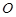 相交于不同的两
相交于不同的两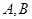 ,在线段
,在线段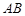 上取一点
上取一点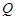 ,满足
,满足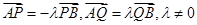 且
且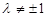 .
. ,
,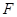 是抛物线
是抛物线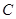 的焦点,过点
的焦点,过点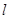 与
与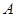 、
、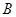 两点,
两点,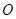 为坐标原点.
为坐标原点.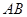 为直径的圆的方程;
为直径的圆的方程;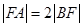 ,求直线
,求直线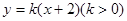 与抛物线
与抛物线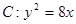 相交于A,B两点,F为C的焦点,若|FA|=2|FB|,则实数k的值为 ( )
相交于A,B两点,F为C的焦点,若|FA|=2|FB|,则实数k的值为 ( )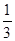
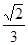
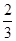
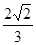
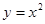 上的点M(
上的点M(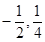 )的切线的倾斜角为( )
)的切线的倾斜角为( )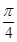
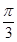

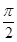
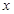 轴为对称轴,以坐标原点为顶点,准线
轴为对称轴,以坐标原点为顶点,准线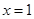 的抛物线的方程是
的抛物线的方程是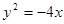
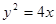
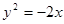
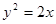
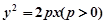 ,过其焦点且斜率为1的
,过其焦点且斜率为1的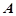 、
、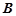 两点,若线段
两点,若线段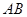 的中点的纵
的中点的纵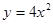 的焦点为圆心,与其准线相切的圆方程是( )
的焦点为圆心,与其准线相切的圆方程是( )