题目内容
6.设x,y∈R,且x>0,y>0,则$({x^2}+\frac{1}{y^2})(\frac{1}{x^2}+4{y^2})$的最小值为9.分析 根据基本不等式的性质求出其最小值即可.
解答 解:$({x^2}+\frac{1}{y^2})(\frac{1}{x^2}+4{y^2})$=5+4x2y2+$\frac{1}{{{x}^{2}y}^{2}}$≥5+2$\sqrt{{{4x}^{2}y}^{2}•\frac{1}{{{x}^{2}y}^{2}}}$=9,
当且仅当xy=$\frac{\sqrt{2}}{2}$时,“=”成立,
故答案为:9.
点评 本题考查了基本不等式的性质,利用性质是注意满足的条件,本题是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.函数f(x)=$\sqrt{1-2cos(2x-\frac{π}{3})}$的单调增区间为( )
| A. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}](k∈Z)$ | B. | [kπ-$\frac{π}{3}$,kπ](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{2π}{3}$](k∈Z) |
16.掷两颗均匀的骰子,则点数之和为7的概率等于( )
| A. | $\frac{1}{18}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
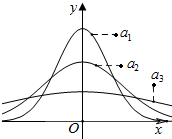 如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3.
如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3. 如图所示,AB是半径为1的圆O的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.
如图所示,AB是半径为1的圆O的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.