题目内容
11.函数f(x)=$\sqrt{1-2cos(2x-\frac{π}{3})}$的单调增区间为( )| A. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}](k∈Z)$ | B. | [kπ-$\frac{π}{3}$,kπ](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{2π}{3}$](k∈Z) |
分析 首先求出函数的定义域,然后在此前提下,求出三角函数cos(2x-$\frac{π}{3}$)的递减区间.
解答 解:f(x)=$\sqrt{1-2cos(2x-\frac{π}{3})}$的定义域为1-2cos(2x-$\frac{π}{3}$)≥0,所以cos(2x-$\frac{π}{3}$)≤$\frac{1}{2}$,
所以2kπ+$\frac{π}{3}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{5π}{3}$,k∈Z,即函数的定义域为[kπ$+\frac{π}{3}$,kπ+π],k∈Z
函数的递增区间为[kπ$+\frac{π}{3}$,kπ+$\frac{2π}{3}$],k∈Z;
故选D.
点评 本题考查了复合函数的单调区间的求法;首先求出函数的定义域,然后在此前提下,求出三角函数cos(2x-$\frac{π}{3}$)相反区间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.数列{an}满足:a1=1,且对每个n∈N*,an,an+1是方程x2+3nx+bn=0的两根,则bn的前6项的和的4倍为( )
| A. | 183 | B. | 132 | C. | 528 | D. | 732 |
2.函数y=$\frac{1}{x}$-x的图象只可能是( )
| A. |  | B. |  | C. |  | D. |  |
3.已知f(x+2)是偶函数,且函数f(x)在[2,+∞)上是单调递增,则( )
| A. | f(3)>f(0) | B. | f(3)>f(1) | C. | f(0)<f(1) | D. | f(4)>f(1) |
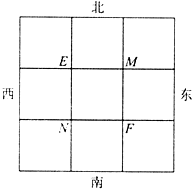 已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.
已知甲、乙两人分别位于图中的M、N两点,每隔1分钟,甲、乙两人分别向东南西北四个方向的其中一个方向行走1格,且甲向四个方向行走的概率是相等的,乙向东、向西行走的概率都是$\frac{1}{3}$,向北行走的概率是$\frac{1}{4}$,甲、乙分别向某个方向行走的事件记为A、B.