题目内容
16．掷两颗均匀的骰子，则点数之和为7的概率等于（ ）| A． | $\frac{1}{18}$ | B． | $\frac{1}{9}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{2}$ |
分析 由题意知本题是一个古典概型，试验发生包含的事件是抛掷两颗骰子，共有6×6种结果，满足条件的事件是点数之和是7，可以列举出所有的事件，共有6种结果，得到概率．
解答 解：由题意知本题是一个古典概型，
试验发生包含的事件是抛掷两颗骰子，共有6×6=36种结果，
满足条件的事件是点数之和是7，可以列举出所有的事件
（1，6）（2，5）（3，4）（4，3）（5，2）（6，1），共有6种结果，
根据古典概型概率公式得到P=$\frac{6}{36}$=$\frac{1}{6}$，
故选：C．
点评 本题考查古典概型，是一个典型的古典概型问题，本题可以列举出试验发生包含的事件和满足条件的事件，应用列举法来解题是大纲对这一部分的要求．
练习册系列答案
相关题目
7．已知f（x）=$\left\{\begin{array}{l}{x，x≥0}\\{1，x＜0}\end{array}\right.$．则不等式f（x2）＞f（3-2x）的解集为（ ）
| A． | （-∞，-1）∪（1，+∞） | B． | （-∞，-3）∪（1，+∞） | C． | （-∞，-3）∪（$\frac{1}{2}$，+∞） | D． | （-∞，-1）∪（$\frac{1}{2}$，+∞） |
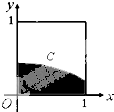在如图所示的正方形中随机取一点，则此点落入阴影部分（曲线C是函数f（x）=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象）的概率为（ ）