已知实数x.y满足条件$\left\{\begin{array}{l}{^{2}≤1}\\{x-y-1≥0}\end{array}\right.$.则z=$\frac{y}{x-2}$的最小值为$\frac{3}{4}$．题目和参考答案——青夏教育精英家教网——

Processing math: 100%

题目内容

17．已知实数x，y满足条件

$\left\{\begin{array}{l}{（x-3）^{2}+（y-2）^{2}≤1}\\{x-y-1≥0}\end{array}\right.$ ，则z=

$\frac{y}{x-2}$ 的最小值为

$\frac{3}{4}$ ．

分析作出不等式组对应的平面区域，利用z的几何意义以及直线的斜率公式即可得到结论

解答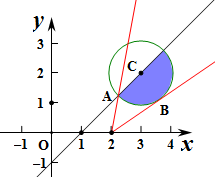解：作出不等式组对应的平面区域阴影部分，如图：
z的几何意义为区域内的点到定点（2，0）的斜率，
由图象可知当直线经过点A时，z取得最大值，当直线与下半圆相切时，
z取得最小值，
由z= $\frac{y}{x-2}$ 得，y=zx-2z，即zx-y-2z=0，
由圆心到直线的距离d= $\frac{|3z-2-2z|}{\sqrt{1+{z}^{2}}}$ =1，
解得z= $\frac{3}{4}$ ，
故z= $\frac{y}{x-2}$ 的最小值为 $\frac{3}{4}$ ；
故答案为： $\frac{3}{4}$ ．

点评本题主要考查线性规划的应用，利用直线和圆的位置关系，以及z的几何意义是解决本题的关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

$\frac{1}{3}$ ，函数y=x（1-3x）的最大值为

$\frac{1}{12}$ ．

8．已知函数f（x）=lnx-ax²-bx．当a=-1时，若函数f（x）在其定义域内是增函数，求b的取值范围．

5．设复数z=a+bi（a，b∈R，a＞0，i是虚数单位），且复数z满足|z|=

$\sqrt{10}$ ，复数（1+2i）z在复平面上对应的点在第一、三象限的角平分线上．
（1）求复数z；
（2）若

$\overline z+\frac{m-i}{1+i}$ 为纯虚数（其中m∈R，

$\overline z=a-bi$ ），求实数m的值．

12．在平面直角坐标系xOy中，直线l的参数方程为：

$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$ （t为参数）．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2

$\sqrt{2}$ sin（θ+

$\frac{π}{4}$ ）．
（Ⅰ）求曲线C的平面直角坐标方程；
（Ⅱ）设直线l与曲线C交于点M，N，若点P的坐标为（1，0），求点P与MN中点的距离．

$\frac{1}{x}$ -x的图象只可能是（　　）

9．已知△ABC中，∠A=

$\frac{π}{6}$ ，AB=3

$\sqrt{3}$ ，AC=3，在线段BC上任取一点P，则线段PB的长大于2的概率为（　　）

$\frac{1}{3}$

$\frac{2}{3}$

$\frac{1}{2}$

$\frac{3}{5}$

6．设x，y∈R，且x＞0，y＞0，则

$（{x^2}+\frac{1}{y^2}）（\frac{1}{x^2}+4{y^2}）$ 的最小值为9．

7．已知f（x）=

$\left\{\begin{array}{l}{x，x≥0}\\{1，x＜0}\end{array}\right.$ ．则不等式f（x²）＞f（3-2x）的解集为（　　）

（-∞，-1）∪（1，+∞）

（-∞，-3）∪（1，+∞）

（-∞，-3）∪（

$\frac{1}{2}$ ，+∞）

（-∞，-1）∪（

$\frac{1}{2}$ ，+∞）