题目内容
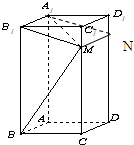
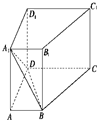
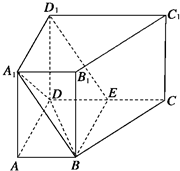
如图，已知在直四棱柱ABCD-A1B1C1D1中，AD⊥DC，AB∥DC，DC=DD1=2AD=2AB=2．
（1）求证：DB⊥平面B1BCC1；
（2）设E是DC上一点，试确定E的位置，使得D1E∥平面A1BD，并说明理由．
（1）求证：DB⊥平面B1BCC1；
（2）设E是DC上一点，试确定E的位置，使得D1E∥平面A1BD，并说明理由．
（1）证明：∵AB∥DC，AD⊥DC，
∴AB⊥AD，在Rt△ABD中，AB=AD=1，
∴BD=
，
易求BC=
，
又∵CD=2，∴BD⊥BC．
又BD⊥BB1，B1B∩BC=B，
∴BD⊥平面B1BCC1．
（2）DC的中点即为E点．
∵DE∥AB，DE=AB，
∴四边形ABED是平行四边形．
∴AD∥BE．
又AD∥A1D1，∴BE∥A1D1，
∴四边形A1D1EB是平行四边形．∴D1E∥A1B．
∵D1E?平面A1BD，
∴D1E∥平面A1BD．
∴AB⊥AD，在Rt△ABD中，AB=AD=1，
∴BD=
| 2 |
易求BC=
| 2 |
又∵CD=2，∴BD⊥BC．
又BD⊥BB1，B1B∩BC=B，
∴BD⊥平面B1BCC1．
（2）DC的中点即为E点．
∵DE∥AB，DE=AB，
∴四边形ABED是平行四边形．
∴AD∥BE．
又AD∥A1D1，∴BE∥A1D1，
∴四边形A1D1EB是平行四边形．∴D1E∥A1B．
∵D1E?平面A1BD，
∴D1E∥平面A1BD．
练习册系列答案
期末集结号系列答案
相关题目
