题目内容
已知实数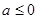 ,函数
,函数 .
.
(I)讨论 在
在 上的奇偶性;
上的奇偶性;
(II)求函数 的单调区间;
的单调区间;
(III)求函数 在闭区间
在闭区间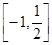 上的最大值。
上的最大值。
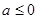 ,函数
,函数 .
.(I)讨论
 在
在 上的奇偶性;
上的奇偶性;(II)求函数
 的单调区间;
的单调区间;(III)求函数
 在闭区间
在闭区间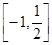 上的最大值。
上的最大值。(I)当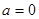 时,
时,  为奇函数;当
为奇函数;当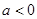 时,
时, 为非奇非偶函数;
为非奇非偶函数;
(II)函数 的增区间
的增区间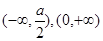 ,函数
,函数 的减区间
的减区间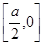 ;
;
(III)当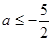 时,
时,  的最大值是
的最大值是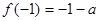
当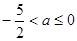 时,
时, 的最大值是
的最大值是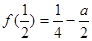 。
。
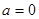 时,
时,  为奇函数;当
为奇函数;当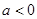 时,
时, 为非奇非偶函数;
为非奇非偶函数;(II)函数
 的增区间
的增区间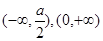 ,函数
,函数 的减区间
的减区间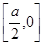 ;
;(III)当
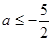 时,
时,  的最大值是
的最大值是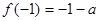
当
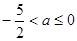 时,
时, 的最大值是
的最大值是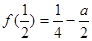 。
。试题分析:(I)当
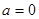 时,
时, 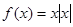 ,因为
,因为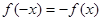 ,故
,故 为奇函数;
为奇函数;当
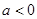 时,
时, 为非奇非偶函数 2分
为非奇非偶函数 2分(II)当
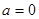 时,
时,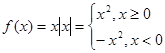 故函数
故函数 的增区间
的增区间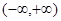 3分
3分当
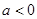 时,
时,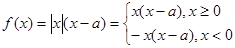
故函数
 的增区间
的增区间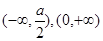 ,函数
,函数 的减区间
的减区间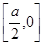 5分
5分(III)①当
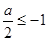 即
即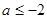 时,
时,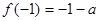 ,
,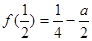
当
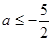 时,
时,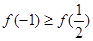 ,
, 的最大值是
的最大值是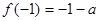
当
 时,
时,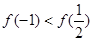 ,
, 的最大值是
的最大值是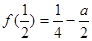 7分
7分② 当
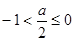 即
即 时,
时,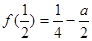 ,
,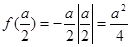 ,
,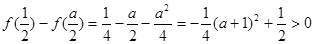 ,
,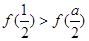
所以,当
 时,
时, 的最大值是
的最大值是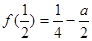 9分
9分综上,当
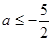 时,
时,  的最大值是
的最大值是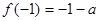
当
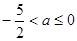 时,
时, 的最大值是
的最大值是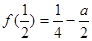 10分
10分点评:中档题,分段函数是高考考查的重点函数类型之一,在不同范围内,函数表达式不同,能有效地扩大考查知识的覆盖面。二次函数的图象和性质也是高考考查的重点。更是阶段考试的主要题型。

练习册系列答案
相关题目
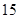 元,销售价是
元,销售价是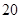 元,月平均销售
元,月平均销售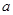 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为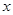
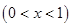 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为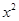 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元).
(元).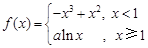 ,其中
,其中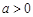
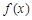 在
在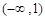 上的单调区间;
上的单调区间;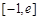 (
(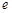 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;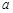 ,曲线
,曲线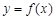 上是否存在两点
上是否存在两点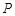 、
、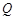 ,使得
,使得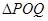 是以原点
是以原点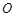 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在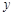 轴上?
轴上?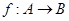 ,其中
,其中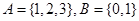 ,已知
,已知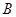 中0的原象是1,则1的原象是
中0的原象是1,则1的原象是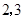
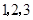
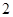 或
或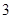 中的一个
中的一个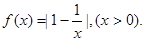
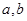
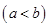 ,使得函数
,使得函数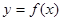 的定义域、值域都是
的定义域、值域都是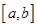 ,若存在,则求出
,若存在,则求出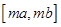 (
(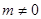 ),求
),求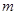 的取值范围.
的取值范围.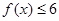 的解集为
的解集为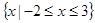 ,求实数
,求实数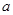 的值;
的值;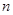 使
使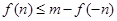 成立,求实数m的取值范围。
成立,求实数m的取值范围。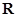 ,其导函数f'(x)的图象如图所示,则对于任意
,其导函数f'(x)的图象如图所示,则对于任意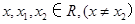 ,下列结论正确的是( )
,下列结论正确的是( )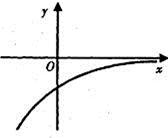
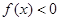 恒成立;
恒成立;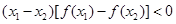 ;
;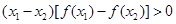 ;
;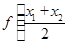 >
> 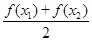 ;
;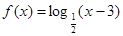 ,则
,则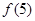 等于
等于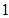
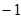
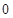
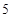
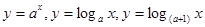 ,
,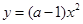 的图象,则与函数
的图象,则与函数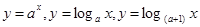 ,
,