题目内容
(本小题满分14分)已知函数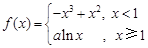 ,其中
,其中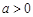
(Ⅰ)求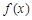 在
在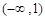 上的单调区间;
上的单调区间;
(Ⅱ)求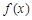 在
在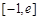 (
(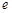 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(III)对任意给定的正实数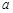 ,曲线
,曲线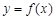 上是否存在两点
上是否存在两点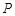 、
、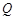 ,使得
,使得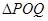 是以原点
是以原点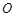 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在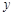 轴上?
轴上?
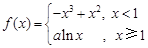 ,其中
,其中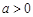
(Ⅰ)求
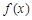 在
在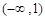 上的单调区间;
上的单调区间;(Ⅱ)求
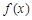 在
在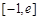 (
(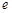 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;(III)对任意给定的正实数
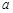 ,曲线
,曲线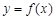 上是否存在两点
上是否存在两点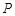 、
、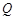 ,使得
,使得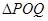 是以原点
是以原点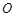 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在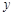 轴上?
轴上?(1)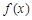 在
在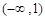 上的单调减区间为
上的单调减区间为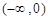 ,
,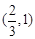 :单调增区间为
:单调增区间为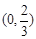
(2)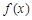 在
在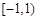 上的最大值为2
上的最大值为2
(3) 对任意给定的正实数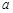 ,曲线
,曲线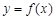 上存在两点
上存在两点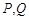 ,使得△
,使得△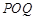 是以
是以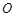 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在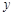 轴上
轴上
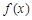 在
在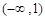 上的单调减区间为
上的单调减区间为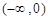 ,
,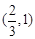 :单调增区间为
:单调增区间为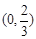
(2)
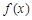 在
在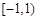 上的最大值为2
上的最大值为2(3) 对任意给定的正实数
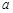 ,曲线
,曲线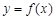 上存在两点
上存在两点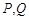 ,使得△
,使得△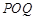 是以
是以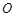 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在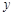 轴上
轴上试题分析:(Ⅰ)因为

当
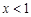 时,
时,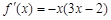 ,
,解
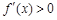 得到
得到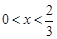 ;解
;解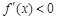 得到
得到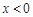 或
或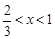 .所以
.所以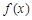 在
在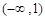 上的单调减区间为
上的单调减区间为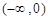 ,
,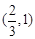 :单调增区间为
:单调增区间为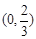 ………………4分
………………4分(Ⅱ)①当
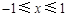 时,由(Ⅰ)知在
时,由(Ⅰ)知在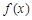
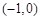 和
和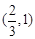 上单调递减,在
上单调递减,在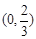 上单调递增,从而
上单调递增,从而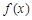 在
在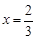 处取得极大值
处取得极大值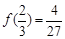 .
.又
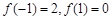 ,所以
,所以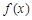 在
在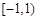 上的最大值为2.……………………6分
上的最大值为2.……………………6分②当
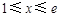 时,
时,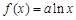 ,当
,当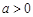 时,
时,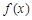 在
在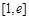 上单调递增,所以
上单调递增,所以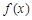 在
在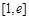 上的最大值为
上的最大值为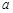 .所以当
.所以当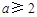 时,
时,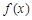 在
在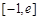 上的最大值为
上的最大值为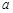 ;当
;当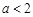 时,
时,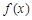 在
在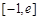 上的最大值为2. …………………………8分
上的最大值为2. …………………………8分(Ⅲ)假设曲线
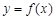 上存在两点
上存在两点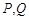 ,使得
,使得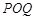 是以
是以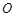 为直角顶点的直角三角形,则
为直角顶点的直角三角形,则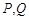 只能在
只能在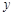 轴的两侧,不妨设
轴的两侧,不妨设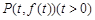 ,则
,则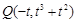 ,且
,且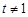 . …9分
. …9分因为
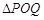 是以
是以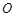 为直角顶点的直角三角形,所以
为直角顶点的直角三角形,所以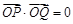 ,
,即:
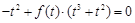 (1) ……………………………………10分
(1) ……………………………………10分是否存在点
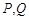 等价于方程(1)是否有解.
等价于方程(1)是否有解.若
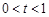 ,则
,则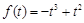 ,代入方程(1)得:
,代入方程(1)得: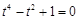 ,此方程无解.…11分
,此方程无解.…11分若
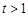 ,则
,则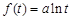 ,代入方程(1)得到:
,代入方程(1)得到: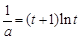 ……12分
……12分设
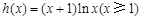 ,则
,则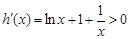 在
在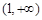 上恒成立.所以
上恒成立.所以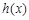 在
在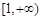 上单调递增,从而
上单调递增,从而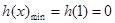 ,即有
,即有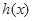 的值域为
的值域为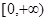 (不需证明),所以当
(不需证明),所以当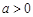 时,方程
时,方程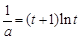 有解,即方程(1)有解.
有解,即方程(1)有解.所以,对任意给定的正实数
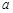 ,曲线
,曲线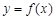 上存在两点
上存在两点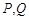 ,使得△
,使得△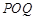 是以
是以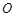 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在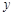 轴上. …………………14分
轴上. …………………14分点评:研究函数中的单调性以及最值问题,一般运用导数的思想,结合导数的符号来判定,进而确定结论,属于中档题。

练习册系列答案
相关题目
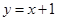
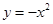
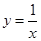
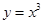
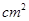 ,画面的宽与高的比为
,画面的宽与高的比为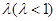 ,画面的上,下各留8
,画面的上,下各留8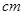 空白,左右各留5
空白,左右各留5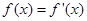 的实数根
的实数根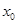 叫做函数
叫做函数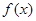 的“新驻点”,若函数
的“新驻点”,若函数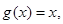
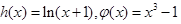 的“新驻点”分别为
的“新驻点”分别为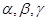 ,则
,则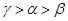
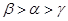
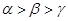
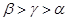
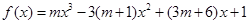 其中
其中
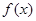 的单调增区间是(0.1),求m的值
的单调增区间是(0.1),求m的值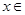
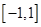 时,函数
时,函数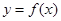 的图像上任意一点的切线斜率恒大于3m,求m的取值范围.
的图像上任意一点的切线斜率恒大于3m,求m的取值范围.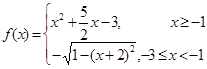 ,则函数
,则函数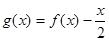 的零点个数为
的零点个数为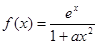 ,其中
,其中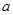 为正实数。
为正实数。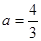 时,求
时,求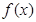 的极值点;
的极值点;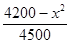 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).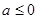 ,函数
,函数 .
. 在
在 上的奇偶性;
上的奇偶性;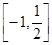 上的最大值。
上的最大值。