题目内容
在△ABC中,AB=5,AC=6,cosA=
,O是△ABC的内心,若
=x
+y
,其中x,y∈[0,1],则动点P的轨迹所覆盖图形的面积为( )
| 1 |
| 5 |
| OP |
| OB |
| OC |
A、
| ||||
B、
| ||||
C、4
| ||||
D、6
|
考点:轨迹方程
专题:计算题,概率与统计
分析:根据向量加法的平行四边形法则,得动点P的轨迹是以OB,OC为邻边的平行四边形,其面积为△BOC面积的2倍.
解答:解:根据向量加法的平行四边形法则,得动点P的轨迹是以OB,OC为邻边的平行四边形,其面积为△BOC面积的2倍.
在△ABC中,由余弦定理可得a2=b2+c2-2bccosA,代入数据,解得BC=7,
设△ABC的内切圆的半径为r,则
bcsinA=
(a+b+c)r,解得r=
,
所以S△BOC=
×BC×r=
×7×
=
,
故动点P的轨迹所覆盖图形的面积为2S△BOC=
.
在△ABC中,由余弦定理可得a2=b2+c2-2bccosA,代入数据,解得BC=7,
设△ABC的内切圆的半径为r,则
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
所以S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
7
| ||
| 3 |
故动点P的轨迹所覆盖图形的面积为2S△BOC=
14
| ||
| 3 |
点评:本题考查轨迹方程,根据向量加法的平行四边形法则,得动点P的轨迹是以OB,OC为邻边的平行四边形,其面积为△BOC面积的2倍是关键.

练习册系列答案
相关题目
三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )


A、2
| ||
B、4
| ||
C、
| ||
D、16
|
已知平面α、β和直线m,给出条件:①m∥α;②m⊥α;③m?α;④α⊥β;⑤α∥β.由这五个条件中的两个同时成立能推导出m∥β的是( )
| A、①④ | B、①⑤ | C、②⑤ | D、③⑤ |
过点P(-1,3),且平行于直线2x-4y+1=0的直线方程为( )
| A、2x+y-5=0 | B、2x+y-1=0 | C、x-2y+7=0 | D、x-2y-5=0 |
直线l:x+
y-4=0与圆C:x2+y2=4的位置关系是( )
| 3 |
| A、相交 | B、相切 |
| C、相离 | D、无法确定 |
某程序框图如图所示,若输入x=
,则该程序运行后输出的a,b值分别是( )

| π |
| 2 |

| A、0,1 | B、1,1 |
| C、1,0 | D、0,0 |
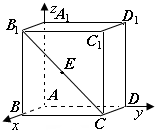 如图,已知正方体ABCD-A1B1C1D1棱长为2,E是线段B1C的中点,分别以AB、AD、AA1为x、y、z轴建立如图所示的空间直角坐标系A-xyz,点E的坐标是
如图,已知正方体ABCD-A1B1C1D1棱长为2,E是线段B1C的中点,分别以AB、AD、AA1为x、y、z轴建立如图所示的空间直角坐标系A-xyz,点E的坐标是