题目内容
直线l:x+
y-4=0与圆C:x2+y2=4的位置关系是( )
| 3 |
| A、相交 | B、相切 |
| C、相离 | D、无法确定 |
考点:直线与圆的位置关系
专题:直线与圆
分析:根据圆心C到直线l的距离正好等于半径,可得直线和圆相切.
解答:解:由于圆心C(0,0)到直线l:x+
y-4=0的距离为
=2,正好等于半径,
故直线和圆相切,
故选:B.
| 3 |
| |0+0-4| | ||
|
故直线和圆相切,
故选:B.
点评:本题主要考查直线和圆相切的性质,点到直线的距离公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知A,B是直径SC=8的球面上的两点,且AB=4,∠BSC=∠ASC=45°,则棱锥S-ABC的体积为( )
A、
| ||||
B、21
| ||||
C、
| ||||
| D、54 |
在△ABC中,AB=5,AC=6,cosA=
,O是△ABC的内心,若
=x
+y
,其中x,y∈[0,1],则动点P的轨迹所覆盖图形的面积为( )
| 1 |
| 5 |
| OP |
| OB |
| OC |
A、
| ||||
B、
| ||||
C、4
| ||||
D、6
|
点P(2+n,2,2-n)到坐标平面XOY的距离是( )
| A、2 | B、2+n | C、6 | D、|2-n| |
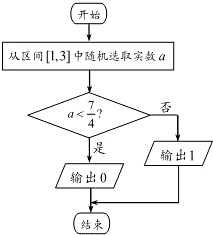
执行如图所示的程序框图,则输出0的概率为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A={(x,y)|(x-4)2+y2≤16}的元素(x0,y0),则满足y0≥x0的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
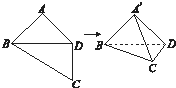 如图,四边形ABCD中,AB=AD=CD=1,BD=
如图,四边形ABCD中,AB=AD=CD=1,BD=