题目内容
过点P（-1，3），且平行于直线2x-4y+1=0的直线方程为（ ）
| A、2x+y-5=0 | B、2x+y-1=0 | C、x-2y+7=0 | D、x-2y-5=0 |
考点：直线的一般式方程与直线的平行关系
专题：直线与圆
分析：由条件利用两直线平行的性质，设出要求的直线的方程为直线方程为2x-4y+c=0，把点P（-1，3），代入求得c的值，可得要求的直线方程．
解答：解：设所求的行于直线2x-4y+1=0的直线方程为2x-4y+c=0，
把点P（-1，3），代入可得-2-12+c=0，c=14，
故要求的直线方程为 2x-4y+14=0，即 x-2y+7=0，
故选：C．
把点P（-1，3），代入可得-2-12+c=0，c=14，
故要求的直线方程为 2x-4y+14=0，即 x-2y+7=0，
故选：C．
点评：本题主要考查利用两直线平行的性质，用待定系数法求直线方程，属于基础题．
练习册系列答案
相关题目
在数列{an}中，设S0=0，Sn=a1+a2+a3+…+an，其中ak=
，1≤k≤n，k，n∈N*，当n≤14时，使Sn=0的n的最大值为 （ ）
|
| A、11 | B、12 | C、13 | D、14 |
已知圆锥的正视图和侧视图都是边长为4的等边三角形，则此圆锥的表面积是（ ）
| A、4π | ||
| B、8π | ||
C、
| ||
| D、12π |
设α为平面，a、b为两条不同的直线，则下列叙述正确的是（ ）
| A、若a∥α，b∥α，则a∥b | B、若a⊥α，a∥b，则b⊥α | C、若a⊥α，a⊥b，则b∥α | D、若a∥α，a⊥b，则b⊥α |
在△ABC中，AB=5，AC=6，cosA=
，O是△ABC的内心，若
=x
+y
，其中x，y∈[0，1]，则动点P的轨迹所覆盖图形的面积为（ ）
| 1 |
| 5 |
| OP |
| OB |
| OC |
A、
| ||||
B、
| ||||
C、4
| ||||
D、6
|
圆O1：x2+y2-2x=0和圆O2：x2+y2-4y=0的公切线条数（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
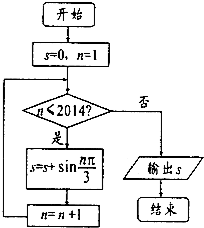
阅读如图所示程序框图，运行相应的程序，则输出的结果是（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
一个盒子里装有标号为1，2，3，4，5的5张标签，随机地选取两张标签，若标签的选取是有放回的，则两张标签上的数字为相邻整数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|