题目内容
在平面直角坐标系xOy中,如果不同的两点A(a,b),B(-a,-b)都在函数y=f(x)的图象上,则称[A,B]为函数y=f(x)的一组“和谐点”([A,B]与[B,A]看成一组),函数g(x)=
的“和谐点”共有 组.
|
考点:分段函数的应用
专题:数形结合法,函数的性质及应用
分析:在同一坐标系内,作出y1=sinx(x>0),y2=|lgx|(x>0)的图象,根据定义,可知函数g(x)=
的“和谐点”的组数,就是图象交点的个数,可得结论.
|
解答:解:由题意,在同一坐标系内,作出y1=sinx(x>0),
y2=|lgx|(x>0)的图象,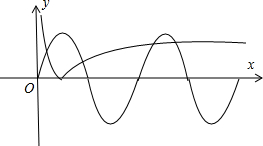
根据定义,可知函数g(x)=
的“和谐点”的组数,就是图象交点的个数,
所以函数g(x)=
的“和谐点”的组数为4.
故答案为:4.
y2=|lgx|(x>0)的图象,

根据定义,可知函数g(x)=
|
所以函数g(x)=
|
故答案为:4.
点评:本题主要考查函数的交点问题,利用定义先求出函数关于原点对称的函数,是解决本题的关键.

练习册系列答案
相关题目
| (2-a)(a+1) |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
方程x3-x-1=0的实数解落在区间( )
| A、(-1,0) | B、(0,1) | C、(2,3) | D、(1,2) |
已知f(x)=
是R上的增函数,那么a的取值范围是( )
|
| A、(0,1) |
| B、(1,5) |
| C、(1,2] |
| D、[2,5) |
在数列{an}中,设S0=0,Sn=a1+a2+a3+…+an,其中ak=
,1≤k≤n,k,n∈N*,当n≤14时,使Sn=0的n的最大值为 ( )
|
| A、11 | B、12 | C、13 | D、14 |
在△ABC中,AB=5,AC=6,cosA=
,O是△ABC的内心,若
=x
+y
,其中x,y∈[0,1],则动点P的轨迹所覆盖图形的面积为( )
| 1 |
| 5 |
| OP |
| OB |
| OC |
A、
| ||||
B、
| ||||
C、4
| ||||
D、6
|