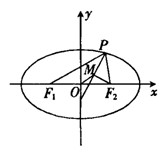
题目内容
已知椭圆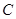 经过点
经过点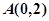 ,
,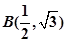 .
.
(Ⅰ)求椭圆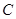 的方程;(Ⅱ)设
的方程;(Ⅱ)设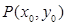 为椭圆
为椭圆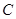 上的动点,求
上的动点,求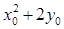 的最大值.
的最大值.
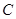 经过点
经过点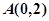 ,
,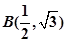 .
.(Ⅰ)求椭圆
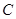 的方程;(Ⅱ)设
的方程;(Ⅱ)设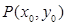 为椭圆
为椭圆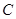 上的动点,求
上的动点,求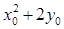 的最大值.
的最大值.(Ⅰ) ;(Ⅱ)4
;(Ⅱ)4
 ;(Ⅱ)4
;(Ⅱ)4试题分析:(Ⅰ)设椭圆方程为
 ,把点
,把点 的坐标代入,得关于
的坐标代入,得关于 的方程组,解方程组求
的方程组,解方程组求 ;](Ⅱ)由(Ⅰ)得椭圆的方程为
;](Ⅱ)由(Ⅰ)得椭圆的方程为 ,因点
,因点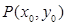 为椭圆
为椭圆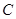 上的动点,有
上的动点,有 ,将
,将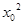 表示出来代入
表示出来代入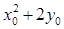 ,可以看成关于
,可以看成关于 的二次函数
的二次函数
 ,转化为求二次函数的最大值求解.
,转化为求二次函数的最大值求解.试题解析:(Ⅰ)设椭圆方程为
 ,把点
,把点 的坐标代入得
的坐标代入得 解得:
解得: ,所以椭圆的方程为
,所以椭圆的方程为 ;
;(Ⅱ)因为P为椭圆上的动点,则
 ,所以
,所以
 ,
, ,∴当
,∴当 时,
时, 取最大值4.
取最大值4.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
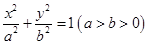 的离心率为
的离心率为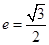 ,直线
,直线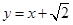 与以原点为圆心、椭圆
与以原点为圆心、椭圆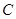 的短半轴长为半径的圆
的短半轴长为半径的圆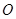 相切.
相切.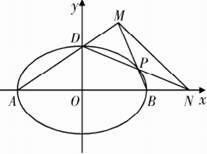
 、
、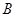 、
、 是椭圆
是椭圆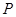 是椭圆
是椭圆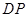 交
交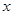 轴于点
轴于点 ,直线
,直线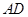 交
交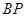 于点
于点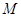 ,设
,设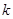 ,
,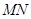 的斜率为
的斜率为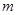 ,求证:
,求证: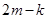 为定值.
为定值.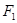 、
、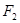 分别是椭圆
分别是椭圆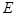 :
: 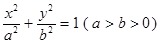 的左、右焦点,点
的左、右焦点,点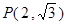 在直线
在直线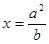 上,线段
上,线段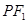 的垂直平分线经过点
的垂直平分线经过点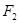 .直线
.直线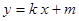 与椭圆
与椭圆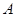 、
、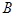 ,且椭圆
,且椭圆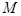 ,使
,使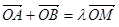 ,其中
,其中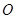 是坐标原点,
是坐标原点,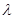 是实数.
是实数.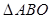 的面积最大?最大面积等于多少?
的面积最大?最大面积等于多少? 的焦点重合,一个顶点的坐标为
的焦点重合,一个顶点的坐标为 ,则此椭圆方程为 .
,则此椭圆方程为 . 外切,同时与圆
外切,同时与圆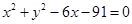 内切,则动圆的圆心在( )
内切,则动圆的圆心在( ) (x≠0)
(x≠0) (x≠0)
(x≠0) (x≠0)
(x≠0) (x≠0)
(x≠0) 与曲线
与曲线 的( )
的( ) 中,已知点
中,已知点 是椭圆
是椭圆 上的一个动点,点
上的一个动点,点 在线段
在线段 的延长线上,且
的延长线上,且 ,则点
,则点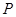 是椭圆
是椭圆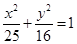 在第一象限上的动点,
在第一象限上的动点,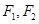 是椭圆的焦点,
是椭圆的焦点,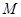 是
是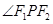 的平分线上的一点,且
的平分线上的一点,且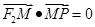 ,则
,则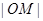 的取值范围是 .
的取值范围是 .