题目内容
已知椭圆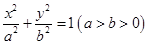 的离心率为
的离心率为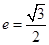 ,直线
,直线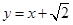 与以原点为圆心、椭圆
与以原点为圆心、椭圆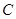 的短半轴长为半径的圆
的短半轴长为半径的圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
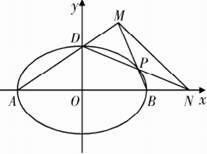
(2)如图, 、
、 、
、 是椭圆
是椭圆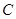 的顶点,
的顶点,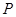 是椭圆
是椭圆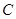 上除顶点外的任意点,直线
上除顶点外的任意点,直线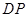 交
交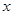 轴于点
轴于点 ,直线
,直线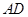 交
交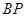 于点
于点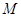 ,设
,设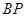 的斜率为
的斜率为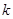 ,
,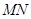 的斜率为
的斜率为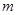 ,求证:
,求证: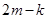 为定值.
为定值.
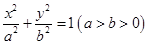 的离心率为
的离心率为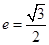 ,直线
,直线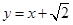 与以原点为圆心、椭圆
与以原点为圆心、椭圆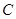 的短半轴长为半径的圆
的短半轴长为半径的圆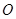 相切.
相切.
(1)求椭圆
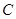 的方程;
的方程;(2)如图,
 、
、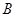 、
、 是椭圆
是椭圆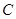 的顶点,
的顶点,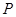 是椭圆
是椭圆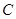 上除顶点外的任意点,直线
上除顶点外的任意点,直线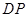 交
交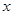 轴于点
轴于点 ,直线
,直线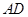 交
交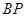 于点
于点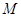 ,设
,设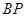 的斜率为
的斜率为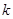 ,
,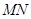 的斜率为
的斜率为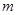 ,求证:
,求证: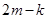 为定值.
为定值.(1)椭圆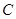 的方程为
的方程为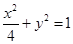 ;(2)详见解析.
;(2)详见解析.
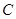 的方程为
的方程为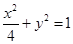 ;(2)详见解析.
;(2)详见解析.试题分析:(1)先根据题中条件求出
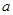 、
、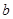 、
、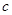 ,进而可以求出椭圆
,进而可以求出椭圆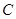 的方程;(2)先由直线
的方程;(2)先由直线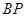 的方程
的方程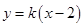 与椭圆的方程联立求出点
与椭圆的方程联立求出点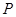 的坐标,然后由
的坐标,然后由 、
、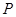 、
、 三点共线,利用平面向量共线进行等价转化,求出点
三点共线,利用平面向量共线进行等价转化,求出点 的坐标,于是得到直线
的坐标,于是得到直线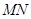 的斜率
的斜率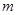 ,最终证明
,最终证明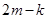 为定值.
为定值.试题解析:(1)由直线
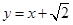 与圆
与圆 得
得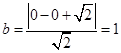 ,
,由
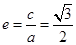 ,得
,得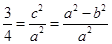 ,所以
,所以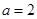 ,
,所以椭圆
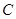 的方程为
的方程为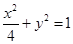 ;
;(2)因为
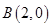 ,
,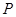 不为椭圆定点,即
不为椭圆定点,即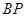 的方程为
的方程为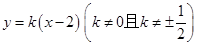 ,①②
,①②将①代入
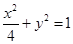 ,解得
,解得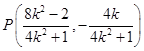 ,
,又直线
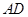 的方程为
的方程为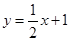 , ②
, ②由
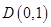 、
、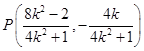 、
、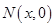 三点共线可得
三点共线可得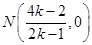 ,
,所以
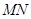 的斜率为
的斜率为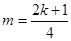 ,则
,则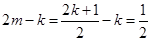 (定值).
(定值).
练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
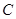 经过点
经过点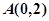 ,
,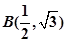 .
.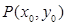 为椭圆
为椭圆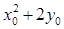 的最大值.
的最大值. 焦点在x轴上,左、右焦眯分别为F1,F2,且|F1F2|=2,点P(1,
焦点在x轴上,左、右焦眯分别为F1,F2,且|F1F2|=2,点P(1,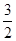 )在椭圆C上.
)在椭圆C上. 的面积为
的面积为 ,求直线l的方程.
,求直线l的方程.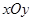 中,点
中,点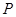 到两点
到两点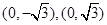 的距离之和等于4,设点
的距离之和等于4,设点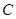 ,直线
,直线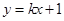 与
与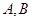 两点.
两点.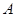 在第一象限,证明当
在第一象限,证明当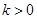 时,恒有
时,恒有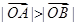 .
.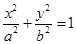
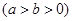 的两个焦点,若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为_____________.
的两个焦点,若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为_____________. 的焦点
的焦点 与椭圆
与椭圆 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为 ,且
,且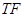 与
与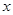 轴垂直,则椭圆的离心率为( )
轴垂直,则椭圆的离心率为( ) 



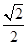
 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于 四点,则四边形
四点,则四边形 面积的最小值为( )
面积的最小值为( )



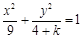 的离心率为
的离心率为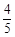 ,则k的值为( )
,则k的值为( ) 或21
或21 或21
或21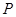 为椭圆
为椭圆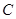 上一点,
上一点,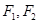 为两焦点,
为两焦点,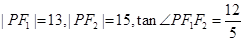 ,则椭圆
,则椭圆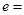 .
.