题目内容
18.过点M(0,1)的直线l与圆心在原点的圆相交于A、B两点,若弦长|AB|=$\sqrt{14}$,△A0B的面积为$\frac{\sqrt{7}}{2}$,求直线l与圆的方程.分析 设直线l为y=kx+1,圆的方程为x2+y2=r2,由点到直线的距离公式和弦长公式,以及三角形的面积公式,就是即可得到所求.
解答 解:直线l的斜率显然存在,设为y=kx+1,
圆的方程为x2+y2=r2,
圆心O到直线的距离为d=$\frac{1}{\sqrt{1+{k}^{2}}}$,①
由弦长公式可得2$\sqrt{{r}^{2}-{d}^{2}}$=$\sqrt{14}$,②
△A0B的面积为S=$\frac{1}{2}$•d•$\sqrt{14}$=$\frac{\sqrt{7}}{2}$,③
解得d=$\frac{\sqrt{2}}{2}$,k=±1,r=2,
即有直线l的方程为y=±x+1,
圆的方程为x2+y2=4.
点评 本题考查直线和圆的方程的求法,考查直线和圆的位置关系,考查点到直线的距离公式和弦长公式,属于中档题.

练习册系列答案
相关题目
8.下列各图中表示的由A到B的对应能构成映射的个数是( )
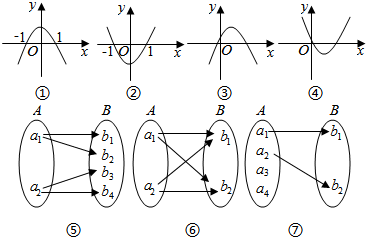

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 △ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求:
△ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求: 在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].
在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].