题目内容
9.己知函数f(x)=ex-x-1(Ⅰ)求函数y=f(x)在点(1,f(1))处的切线方程:
(Ⅱ)若方程f(x)=a,在[-2,ln 2]上有唯一零点,求实数a的取值范围;
(Ⅲ)对任意x≥0,f(x)≥(t-1)x恒成立,求实数t的取值范闱.
分析 (Ⅰ)求导数,确定切线的斜率,即可求出函数y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)函数f(x)=a,在[-2,ln2]上有唯一零点,等价于,f(ln2)<a≤f(-2)或a=f(0),即可求实数a的取值范围;
(Ⅲ)令g(x)=f(x)-(t-1)x=ex-1-tx,则g′(x)=ex-t,分类讨论,确定函数的单调性,即可求实数t的取值范闱.
解答 解:(Ⅰ)∵f(x)=ex-x-1,
∴f′(x)=ex-1.…(1分)
∴f′(1)=e-1,f(1)=e-2,
∴求函数y=f(x)在点(1,f(1))处的切线方程是y-(e-2)=(e-1)(x-1).
化简得所求切线的方程为y=(e-1)x-1.…(3分)
(Ⅱ)f′(x)=ex-1,
当x∈(-2,0)时,f′(x)≤0,f(x)单调递减;
当x∈(0,ln2)时,f′(x)≥0,f(x)单调递增.…(5分)
$f(-2)=\frac{1}{e^2}+1$,f(ln2)=1-ln2.…(6分)
∵f(-2)>f(ln2).
函数f(x)=a,在[-2,ln2]上有唯一零点,等价于,f(ln2)<a≤f(-2)或a=f(0),
即$1-ln2<a≤1+\frac{1}{e^2}$或a=0.
∴实数a的取值范围是$1-ln2<a≤1+\frac{1}{e^2}$或a=0.…(8分)
(Ⅲ)令g(x)=f(x)-(t-1)x=ex-1-tx,则g′(x)=ex-t.
∵x≥0,∴ex≥1.…(9分)
( i)当t≤1时,g′(x)≥0,g(x)在区间[0,+∞)上是增函数,所以g(x)≥g(0)=0.
即f(x)≥(t-1)x恒成立.…(11分)
( ii)当t>1时,ex-t=0,x=lnt,
当x∈(0,lnt)时,g′(x)≤0,g(x)单调递减,
当x∈(0,lnt)时,g(x)<g(0)=0,此时不满足题设条件.…(12分)
综上所述:实数t的取值范围是t≤1.…(13分)
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的零点,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

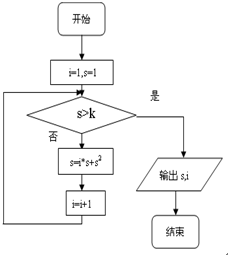
| A. | 88 | B. | 89 | C. | 8095 | D. | 8096 |
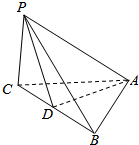 如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.
如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.