题目内容
3. 在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].
在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上变动(如图所示),若$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,其中λ,μ∈R.则2λ-μ的取值范围是[-1,1].
分析 建立如图所示的坐标系,则A(0,0),E(1,0),D(0,1),F(1.5,0.5),P(cosα,sinα)(0°≤α≤90°),λ,μ用参数进行表示,利用辅助角公式化简,即可得出结论.
解答 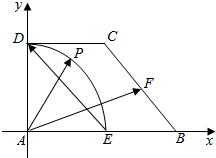 解:建立如图所示的坐标系,则A(0,0),E(1,0),D(0,1),F(1.5,0.5),P(cosα,sinα)(0°≤α≤90°),
解:建立如图所示的坐标系,则A(0,0),E(1,0),D(0,1),F(1.5,0.5),P(cosα,sinα)(0°≤α≤90°),
∵$\overrightarrow{AP}$=λ$\overrightarrow{ED}$+μ$\overrightarrow{AF}$,
∴(cosα,sinα)=λ(-1,1)+μ(1.5,0.5),
∴cosα=-λ+1.5μ,sinα=λ+0.5μ,
∴λ=$\frac{1}{4}$(3sinα-cosα),μ=$\frac{1}{2}$(cosα+sinα),
∴2λ-μ=sinα-cosα=$\sqrt{2}$sin(α-45°)
∵0°≤α≤90°,
∴-45°≤α-45°≤45°,
∴-$\frac{\sqrt{2}}{2}$≤sin(α-45°)≤$\frac{\sqrt{2}}{2}$,
∴-1≤$\sqrt{2}$sin(α-45°)≤1
∴2λ-μ的取值范围是[-1,1].
故答案为:[-1,1].
点评 本题考查平面向量知识的运用,考查学生的计算能力,正确利用坐标系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知随机变量X服从正态分布N(3,1),且P(X>4)=0.1587,则P(2≤X≤4)等于( )
| A. | 0.3413 | B. | 0.1585 | C. | 0.8413 | D. | 0.6826 |
12.定义运算“*”如下:x*y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=(1-2x)*(2x-3),则f(x)等于( )
| A. | $\left\{\begin{array}{l}1-{2}^{x},x≤1\\{2}^{x}-3,x>1\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{2}^{x}-3,x<1}\\{1-{2}^{x},x≥1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{{2}^{x}-4,x≥1}\\{2-{2}^{x},x<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{{4}^{x}-3,x<1}\\{1-{4}^{x},x≥1}\end{array}\right.$ |