题目内容
10.已知函数f(x)=ax2+1,g(x)=x3+bx,其中a>0,b>0.(Ⅰ)若曲线y=f(x)与曲线y=g(x)在它们的交点P(2,m)处有相同的切线(P为切点),求a,b的值;
(Ⅱ)令h(x)=f(x)+g(x),若函数h(x)的单调递减区间为[-$\frac{a}{2}$,-$\frac{\sqrt{b}}{3}$],
(1)求函数h(x)在区间(-∞,-1]上的最大值t(a);
(2)若|h(x)|≤3在x∈[-2,0]上恒成立,求实数a的取值范围.
分析 (Ⅰ)根据曲线y=f(x)与曲线y=g(x)在它们的交点(2,m)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;
(Ⅱ)(1)根据函数h(x)的单调递减区间为[-$\frac{a}{2}$,-$\frac{\sqrt{b}}{3}$]得出a2=4b,构建函数h(x)=f(x)+g(x)=x3+ax2+$\frac{1}{4}$a2x+1,求导函数,利用导数的正负,可确定函数的单调区间,进而分类讨论,确定函数在区间(-∞,-1]上的最大值.
(2)由(1)知,函数h(x)在(-∞,-$\frac{a}{2}$)单调递增,在(-$\frac{a}{2}$,-$\frac{a}{6}$)单调递减,在(-$\frac{a}{6}$,+∞)上单调递增,从而得出其极大值、极小值,再根据|h(x)|≤3,在x∈[-2,0]上恒成立,建立关于a的不等关系,解得a的取值范围即可.
解答 解:(Ⅰ)f(x)=ax2+1(a>0),则f′(x)=2ax,k1=4a,g(x)=x3+bx,则f′(x)=3x2+b,k2=12+b,
由(2,m)为公共切点,可得:4a=12+b,
又f(2)=4a+1,g(2)=8+2b,
∴4a+1=8+2b,与4a=12+b联立可得:a=$\frac{17}{4}$,b=5.
(Ⅱ)由h(x)=f(x)+g(x)=x3+ax2+bx+1,
则h′(x)=3x2+2ax+b,
∵函数h(x)的单调递减区间为[-$\frac{a}{2}$,-$\frac{\sqrt{b}}{3}$],∴当x∈[-$\frac{a}{2}$,-$\frac{\sqrt{b}}{3}$]时,3x2+2ax+b≤0恒成立,
此时,x=-$\frac{\sqrt{b}}{3}$是方程3x2+2ax+b=0的一个根,得3($-\frac{\sqrt{b}}{3}$)2+2a(-$\frac{\sqrt{b}}{3}$)+b=0,得a2=4b,
∴h(x)=x3+ax2+$\frac{1}{4}$a2x+1
令h′(x)=0,解得:x1=-$\frac{a}{2}$,x2=-$\frac{a}{6}$;
∵a>0,∴-$\frac{a}{2}$<-$\frac{a}{6}$,列表如下:
| x | (-∞,-$\frac{a}{2}$) | -$\frac{a}{2}$ | (-$\frac{a}{2}$,-$\frac{a}{6}$) | -$\frac{a}{6}$ | (-$\frac{a}{6}$,+∞) |
| h′(x) | + | - | + | ||
| h(x) | 极大值 | 极小值 |
①若-1≤-$\frac{a}{2}$,即a≤2时,最大值为t(-1)=a-$\frac{{a}^{2}}{4}$;
②若-$\frac{a}{2}$<-1<-$\frac{a}{6}$,即2<a<6时,最大值为t(-$\frac{a}{2}$)=1
③若-1≥-$\frac{a}{6}$时,即a≥6时,最大值为t(-$\frac{a}{2}$)=1.
综上所述:当a∈(0,2]时,最大值为t(-1)=a-$\frac{{a}^{2}}{4}$;
当a∈(2,+∞)时,最大值为t(-$\frac{a}{2}$)=1.
(2)由(1)知,函数h(x)在(-∞,-$\frac{a}{2}$)单调递增,在(-$\frac{a}{2}$,-$\frac{a}{6}$)单调递减,在(-$\frac{a}{6}$,+∞)上单调递增,
故h(-$\frac{a}{2}$)为极大值,h(-$\frac{a}{2}$)=1;h(-$\frac{a}{6}$)为极小值,h(-$\frac{a}{6}$)=-$\frac{{a}^{3}}{54}$+1;
∵|h(x)|≤3,在x∈[-2,0]上恒成立,又h(0)=1.
∴$\left\{\begin{array}{l}{h(-2)≥-3}\\{h(-\frac{a}{6})≥-3}\end{array}\right.$,即$\left\{\begin{array}{l}{-\frac{1}{2}{a}^{2}+4a-7≥-3}\\{-\frac{{a}^{3}}{54}+1≥-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{4-2\sqrt{2}≤a≤4+2\sqrt{2}}\\{a≤6}\end{array}\right.$,
∴a的取值范围:4-2$\sqrt{2}$≤a≤6.
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,解题的关键是正确求出导函数和应用分类讨论的方法,属难题.

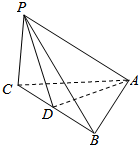 如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.
如图,△ABC是边长为2的等边三角形,PC⊥底面ABC,PC=2$\sqrt{2}$,求PA与侧面PBC所成角的大小.