题目内容
设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=lo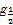 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( )
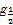 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( )| A.是增函数,且f(x)<0 |
| B.是增函数,且f(x)>0 |
| C.是减函数,且f(x)<0 |
| D.是减函数,且f(x)>0 |
D
【思路点拨】根据f(x)是周期为2的偶函数,把x∈(1,2)转化到2-x∈(0,1)上,再利用f(2-x)=f(x)求解.
解:由题意得当x∈(1,2)时,0<2-x<1,0<x-1<1,f(x)=f(-x)=f(2-x)
=lo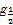 [1-(2-x)]=lo
[1-(2-x)]=lo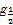 (x-1)>lo
(x-1)>lo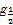 1=0,则可知当x∈(1,2)时,f(x)是减函数,选D.
1=0,则可知当x∈(1,2)时,f(x)是减函数,选D.
解:由题意得当x∈(1,2)时,0<2-x<1,0<x-1<1,f(x)=f(-x)=f(2-x)
=lo
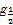 [1-(2-x)]=lo
[1-(2-x)]=lo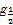 (x-1)>lo
(x-1)>lo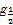 1=0,则可知当x∈(1,2)时,f(x)是减函数,选D.
1=0,则可知当x∈(1,2)时,f(x)是减函数,选D.
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ,
, ,
, .
. ,设函数
,设函数 ,求
,求 的极大值;
的极大值;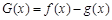 ,讨论
,讨论 的单调性.
的单调性. 满足
满足 ,
, ,设函数
,设函数
 时,求
时,求 的极小值;
的极小值; (
( )的极小值点与
)的极小值点与 的极大值小于等于
的极大值小于等于
 的导函数如图所示,若
的导函数如图所示,若 为锐角三角形,则下列不等式一定成立的是( )
为锐角三角形,则下列不等式一定成立的是( )




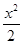 -2x+5,若对任意的x∈[-1,2],都有f(x)>m,则实数m的取值范围为________.
-2x+5,若对任意的x∈[-1,2],都有f(x)>m,则实数m的取值范围为________. )上是减函数,在(
)上是减函数,在(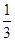 x3-
x3-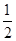 ax2+(a-1)x+1在区间(1,5)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围是( )
ax2+(a-1)x+1在区间(1,5)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围是( )