题目内容
已知实数 满足
满足 ,
, ,设函数
,设函数
(1)当 时,求
时,求 的极小值;
的极小值;
(2)若函数 (
( )的极小值点与
)的极小值点与 的极小值点相同,求证:
的极小值点相同,求证: 的极大值小于等于
的极大值小于等于
 满足
满足 ,
, ,设函数
,设函数
(1)当
 时,求
时,求 的极小值;
的极小值;(2)若函数
 (
( )的极小值点与
)的极小值点与 的极小值点相同,求证:
的极小值点相同,求证: 的极大值小于等于
的极大值小于等于
(1)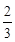 ;(2)见解析
;(2)见解析
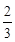 ;(2)见解析
;(2)见解析试题分析:(1)把
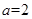 代入原函数先得解析式,再求导数,列表判断单调性求函数的极小值;(2)先分别求函数
代入原函数先得解析式,再求导数,列表判断单调性求函数的极小值;(2)先分别求函数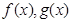 的导函数,再分
的导函数,再分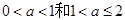 两种情况讨论,根据条件函数
两种情况讨论,根据条件函数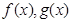 的极小值点相同分别求
的极小值点相同分别求 的极大值,从而进行判断得结论
的极大值,从而进行判断得结论试题解析:(Ⅰ) 解: 当a=2时,f ′(x)=x2-3x+2=(x-1)(x-2)
列表如下:
| x | (-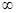 ,1 ,1 ) ) | 1 | (1,2) | 2 | (2,+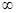 ) ) |
| f ′(x) | + | 0 | - | 0 | + |
| f (x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
所以,f (x)极小值为f (2)=
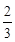 5分
5分(Ⅱ) 解:f ′(x)=x2-(a+1)x+a=(x-1)(x-a)
g ′(x)=3x2+2bx-(2b+4)+
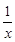 =
=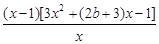
令p(x)=3x2+(2b+3)x-1,
(1)当 1<a≤2时,
f(x)的极小值点x=a,则g(x)的极小值点也为x=a,
所以pA=0,
即3a2+(2b+3)a-1=0,
即b=
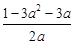 ,
,此时g(x)极大值=g(1)=1+b-(2b+4)=-3-b
=-3+
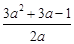 =
=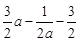
由于1<a≤2,
故
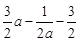 ≤
≤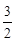
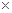 2-
2- -
-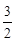 =
= 10分
10分(2)当0<a<1时,
f(x)的极小值点x=1,则g(x)的极小值点为x=1,
由于p(x)=0有一正一负两实根,不妨设x2<0<x1,
所以0<x1<1,
即p(1)=3+2b+3-1>0,
故b>-
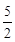
此时g(x)的极大值点x=x1,
有 g(x1)=x13+bx12-(2b+4)x1+lnx1
<1+bx12-(2b+4)x1
=(x12-2x1)b-4x1+1 (x12-2x1<0)
<-
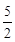 (x12-2x1)-4x1+1
(x12-2x1)-4x1+1=-
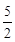 x12+x1+1
x12+x1+1=-
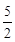 (x1-
(x1-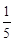 )2+1+
)2+1+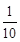 (0<x1<1)
(0<x1<1)≤
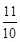 <
<
综上所述,g(x)的极大值小于等于
 14分
14分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
 .
. .的单调区间;
.的单调区间; 的极值.
的极值.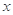 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为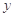 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用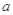 亿元,至多
亿元,至多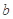 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用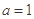 ,
,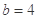 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=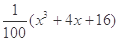 作为生态环境改造投资方案.
作为生态环境改造投资方案.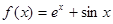 ,
,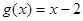 ;
;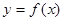 在
在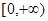 上单调递增;
上单调递增;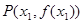 ,
,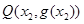
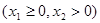 ,若直线
,若直线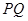
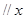 轴,求
轴,求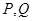 两点间的最短距离.
两点间的最短距离. 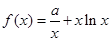 ,
, .
.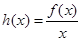 的单调性;
的单调性;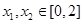 ,使得
,使得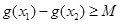 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数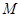 ;
;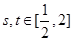 ,都有
,都有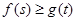 成立,求实数
成立,求实数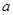 的取值范围.
的取值范围.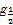 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( ) 的单调增区间是 .
的单调增区间是 .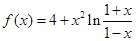 在区间
在区间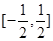 上的最大值与最小值分别为
上的最大值与最小值分别为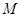 和
和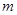 ,则
,则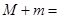 .
.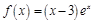 的单调递增区间是( )
的单调递增区间是( )