题目内容
1．在△ABC中，∠C=90°，CD是斜边上的高，已知CD=60，AD=25，求BD=144．分析 由射影定理可得：CD2=AD•BD，代入解出即可．
解答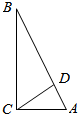 
解：如图所示，
由射影定理可得：
CD2=AD•BD，
∴$BD=\frac{C{D}^{2}}{AD}$=$\frac{6{0}^{2}}{25}$=144．
故答案为：144．
点评 本题考查了射影定理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
16．已知sinα-cosα=$\frac{1}{2}$，且α∈（0，π），则sinα+cosα=（ ）
| A． | $\frac{{\sqrt{7}}}{2}$ | B． | $-\frac{{\sqrt{7}}}{2}$ | C． | $±\frac{{\sqrt{7}}}{2}$ | D． | $±\frac{1}{2}$ |
13．△ABC中，$\frac{a}{cosA}$=$\frac{b}{cosB}$=$\frac{c}{cosC}$，则△ABC一定是（ ）
| A． | 直角三角形 | B． | 钝角三角形 | C． | 等腰三角形 | D． | 等边三角形 |
10．函数f（x）=ax3+bx2+1，在x=1处取得极大值3，则f（x）的极小值为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
11．已知曲线C的方程为x2+x+y-1=0，则下列各点中在曲线C上的点是（ ）
| A． | （0，1） | B． | （-1，3） | C． | （1，1） | D． | （-1，1） |