Question

【题目】设，是的两个非空子集，如果存在一个函数满足：① ；② 对任意，当时，恒有，那么称这两个集合为“到的保序同构”，以下集合对不是“到的保序同构”的是（ ）

A.B.，

C.，D.，

Answer 1

【答案】D

【解析】

由题意可知S为函数的一个定义域，T为其所对应的值域，且函数y＝f（x）为单调增函数，对题目给出的4个选项中的集合逐一分析看是否能找到这样的函数y＝f（x）即可．

对于A中的两个集合，可取函数f（x）＝x-1，x∈，满足：（i）B＝{f（x）|x∈A}；（ii）对任意x1，x2∈A，当x1＜x2时，恒有f（x1）＜f（x2），故A是“保序同构”；

对于B中的两个集合，可取函数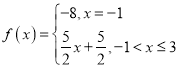 满足题意,是“保序同构”；

对于C中的两个集合，可取函数f（x） （0＜x＜1），是“保序同构”．利用排除法可知选：D

故选：D．